
分析 (1)根据优惠政策,第一次购物不打折.设出第二次购物的实际价值为x元,根据题意列出关于x的方程,求出方程的解得到x的值,求出两次购物的实际价值,即可得到结果.
(2)利用“应该支付的费用-实际支付的费用”进行计算;
(3)一次性消费了654元,则其中500元按9折优惠,超出的部分按8折优惠.
解答 解:(1)∵134<200,
∴第一次购物不打折.
设第二次购物的实际价值为x元,则
500×90%+(x-500)×80%=466,
解得:x=520,
答:此人两次所购物品的实际价值分别为:134元、520元;
(2)520-466=54(元).
答:这次活动中他节省了54元钱;
(3)若一次性购买这些商品,应付520+134=654>500,实际付(654-500)×80%+500×90%=573.2(元),
比分开买节省(466+134)-573.2=26.8(元).
即一次性购买更省钱.
点评 本题考查了一元一次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
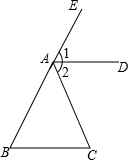 如图,∠CAE是△ABC的外角,
如图,∠CAE是△ABC的外角,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
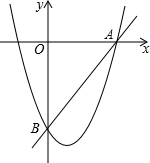 如图,抛物线y=x2+bx-4分别与x轴正半轴、y轴交于点A、B,且$tan∠OBA=\frac{3}{4}$.
如图,抛物线y=x2+bx-4分别与x轴正半轴、y轴交于点A、B,且$tan∠OBA=\frac{3}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
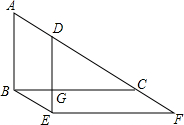 如图,直角三角形△ABC沿着AC所在直线平移得到△DEF,
如图,直角三角形△ABC沿着AC所在直线平移得到△DEF,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com