
分析 先根据一次函数图象上点的坐标特征,把A(-5,y)、B(x,0)分别代入y=-$\frac{3}{4}$x-$\frac{3}{4}$,求出x与y的值,得到A、B两点的坐标,再分AB=AC,BA=BC,CA=CB三种情况即可求出y轴上点C的坐标.
解答 解:∵A(-5,y)、B(x,0)都在直线y=-$\frac{3}{4}$x-$\frac{3}{4}$上,
∴y=-$\frac{3}{4}$×(-5)-$\frac{3}{4}$=3,
0=-$\frac{3}{4}$x-$\frac{3}{4}$,解得x=-1,
∴A(-5,3)、B(-1,0).
设y轴上点C的坐标是(0,t),当三角形ABC是等腰三角形时,分三种情况:
①如果AB=AC,
那么(-1+5)2+(0-3)2=(0+5)2+(t-3)2,
解得t=3,
所以点C的坐标是(0,3);
②如果BA=BC,
那么(-1+5)2+(0-3)2=(0+1)2+(t-0)2,
解得t=±2$\sqrt{6}$,
所以点C的坐标是(0,2$\sqrt{6}$)或(0,-2$\sqrt{6}$);
③如果CA=CB,
那么(0+5)2+(t-3)2=(0+1)2+(t-0)2,
解得t=5.5,
所以点C的坐标是(0,5.5).
综上所述,所求点C的坐标是(0,3)或(0,2$\sqrt{6}$)或(0,-2$\sqrt{6}$)或(0,5.5).
故答案为(0,3)或(0,2$\sqrt{6}$)或(0,-2$\sqrt{6}$)或(0,5.5).
点评 本题考查了一次函数图象上点的坐标特征,等腰三角形的性质,勾股定理,正确求出A、B两点的坐标以及分类讨论是解题的关键.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题
| 销售单价x(元) | 12 | 14 | 16 | 18 |
| 年销售量y(万件) | 7 | 6 | 5 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
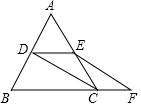 如图,△ABC是等边三角形,点D,E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连接CD和EF,求证:四边形DEFC是平行四边形.
如图,△ABC是等边三角形,点D,E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连接CD和EF,求证:四边形DEFC是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | 3 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
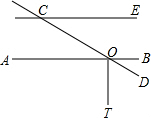
| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省襄阳市九年级下学期第一次月考数学试卷(解析版) 题型:单选题
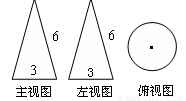
一个几何体的三视图如图,其中主视图都是腰长为6、底边长为3的等腰三角形,则这个几何体的侧面展开图的面积为( )
A. 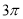 B.
B. 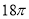 C.
C. 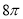 D.
D. 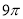
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com