
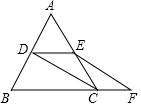
 如图,△ABC是等边三角形,点D,E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连接CD和EF,求证:四边形DEFC是平行四边形.
如图,△ABC是等边三角形,点D,E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连接CD和EF,求证:四边形DEFC是平行四边形. 科目:初中数学 来源: 题型:选择题
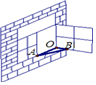 如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )| A. | 垂线段最短 | B. | 两点之间线段最短 | ||
| C. | 两点确定一条直线 | D. | 三角形的稳定性 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
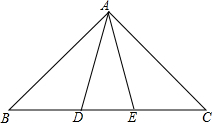 如图,△ABC中,AB=AC,点D,E在边BC上,且BD=CE.
如图,△ABC中,AB=AC,点D,E在边BC上,且BD=CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月份 | 一 | 二 | 三 | 四 |
| 用水量(吨) | 6 | 7 | 12 | 15 |
| 水费(元) | 12 | 14 | 28 | 37 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2017届浙江省九年级3月模拟数学试卷(解析版) 题型:填空题
在△ABC中,若三边BC , CA, AB满足 BC︰CA︰AB=5︰12︰13,则cosB=_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com