
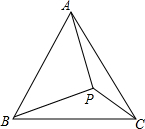
 如图,P为等边三角形ABC内一点,PC=3,PA=4,PB=5,求∠APC的度数.
如图,P为等边三角形ABC内一点,PC=3,PA=4,PB=5,求∠APC的度数. 分析 首先将△BCP绕点C顺时针旋转60°得△ACQ,连接PQ.再过A作CP的延长线的垂线AD,垂足为D,易证得△PCQ是等边三角形,△APQ是直角三角形,则可求得∠APC的度数,然后可求得∠APD的度数,在Rt△APD中,即可求得AD与CD的长,继而求得AC.
解答 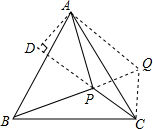 解:将△BCP绕点C顺时针旋转60°得△ACQ,连接PQ.再过A作CP的延长线的垂线AD,垂足为D,
解:将△BCP绕点C顺时针旋转60°得△ACQ,连接PQ.再过A作CP的延长线的垂线AD,垂足为D,
∴AQ=PB=5,CQ=PC,∠PCQ=60°,
∴△PCQ是等边三角形,
∴PQ=PC=3,∠QPC=60°,
在△PAQ中,∵PA=4,AQ=5,PQ=3,
∴AQ2=PA2+PQ2,
∴∠APQ=90°,
∴∠APC=∠APQ+∠QPC=150°.
点评 此题考查了等边三角形的判定与性质、勾股定理的逆定理以及直角三角形的性质.此题难度较大,注意掌握辅助线的作法,注意数形结合思想的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
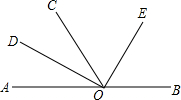 如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC.
如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
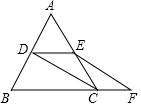 如图,△ABC是等边三角形,点D,E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连接CD和EF,求证:四边形DEFC是平行四边形.
如图,△ABC是等边三角形,点D,E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连接CD和EF,求证:四边形DEFC是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 回收废旧报纸的质量/千克 | 1.5 | 2 | 3.5 | 4 | … |
| 付款全额/元 | 0.75 | 1.0 | 1.9 | 2.2 | … |
查看答案和解析>>
科目:初中数学 来源:2017届浙江省九年级3月模拟数学试卷(解析版) 题型:判断题
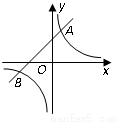
如图,反比例函数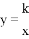 的图象与一次函数
的图象与一次函数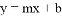 的图象交于
的图象交于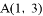 ,
,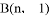 两点.
两点.
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当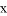 取何值时,反比例函数的值大于一次函数的值.
取何值时,反比例函数的值大于一次函数的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com