
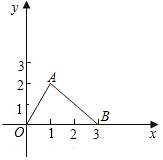
 如图,在平面直角坐标系中,点A在第一象限,点A的横坐标为1,OA=2,求点A的坐标.
如图,在平面直角坐标系中,点A在第一象限,点A的横坐标为1,OA=2,求点A的坐标.  名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
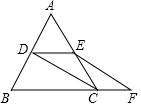 如图,△ABC是等边三角形,点D,E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连接CD和EF,求证:四边形DEFC是平行四边形.
如图,△ABC是等边三角形,点D,E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连接CD和EF,求证:四边形DEFC是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
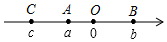 如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:
如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | 3 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
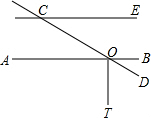
| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
查看答案和解析>>
科目:初中数学 来源:2017届浙江省九年级3月模拟数学试卷(解析版) 题型:单选题
二次函数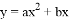 的图象如图,若一元二次方程
的图象如图,若一元二次方程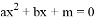 有实数根,则以下关于
有实数根,则以下关于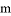 的结论正确的是( )
的结论正确的是( )
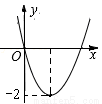
A. m的最大值为2 B. m的最小值为-2
C. m是负数 D. m是非负数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com