
【题目】如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG交BE于点H,连接DH,下列结论正确的个数是( )
①△ABG∽△FDG ②HD平分∠EHG ③AG⊥BE ④S△HDG:S△HBG=tan∠DAG ⑤线段DH的最小值是2 ![]() ﹣2.
﹣2.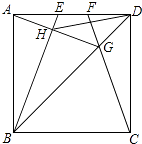
A.2
B.3
C.4
D.5
【答案】C
【解析】∵四边形ABCD是正方形,
∴AB=CD,∠BAD=∠ADC=90°,∠ADB=∠CDB=45°,
在△ABE和△DCF中,
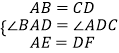 ,
,
∴△ABE≌△DCF(SAS),
∴∠ABE=∠DCF,
在△ADG和△CDG中,
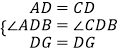 ,
,
∴△ADG≌△CDG(SAS),
∴∠DAG=∠DCF,
∴∠ABE=∠DAG,
∵∠DAG+∠BAH=90°,
∴∠BAE+∠BAH=90°,
∴∠AHB=90°,
∴AG⊥BE,故③正确,
同法可证:△AGB≌△CGB,
∵DF∥CB,
∴△CBG∽△FDG,
∴△ABG∽△FDG,故①正确,
∵S△HDG:S△HBG=DG:BG=DF:BC=DF:CD=tan∠FCD,
又∵∠DAG=∠FCD,
∴S△HDG:S△HBG=tan∠FCD=tan∠DAG,故④正确
取AB的中点O,连接OD、OH, 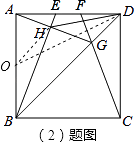
∵正方形的边长为4,
∴AO=OH= ![]() ×4=2,
×4=2,
由勾股定理得,OD= ![]() =2
=2 ![]() ,
,
由三角形的三边关系得,O、D、H三点共线时,DH最小,
DH最小=2 ![]() ﹣2.
﹣2.
无法证明DH平分∠EHG,故②错误,
故①③④⑤正确,
所以答案是:C.
【考点精析】关于本题考查的正方形的性质和相似三角形的判定与性质,需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
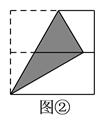
【题目】如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形(阴影部分),且它的一条直角边等于斜边的一半,这样的图形有( ).



A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知BD= ![]() ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一个月用水10 t以内(包括10 t)的用户,每吨收水费a元;一个月用水超过10 t的用户,10 t水仍按每吨a元收费,超过10 t的部分,按每吨b(b>a)元收费.设一户居民月用水x t,应交水费y元,y与x之间的函数关系如图所示.
(1)求a的值;某户居民上月用水8 t,应交水费多少元?
(2)求b的值,并写出当x>10时,y与x之间的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC中,在射线BA上有一点D,连接CD,并以CD为边向上作等边△CDE,连接BE和AE.试判断下列结论:①AE=BD; ②AE与AB所夹锐夹角为60°;③当D在线段AB或BA延长线上时,总有∠BDE-∠AED=2∠BDC;④∠BCD=90°时,CE2+AD2=AC2+DE2 .正确的序号有( )

A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:
(1)汽车在前9分钟内的平均速度是多少?
(2)汽车在中途停了多长时间?
(3)当16≤t≤30时,求S与t的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数a,b,c在数轴上对应的点分别为A,B,C,且满足(a-1)2+|ab+3|=0,c=-2a+b.
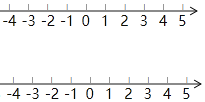
(1)分别求a,b,c的值;
(2)若点A和点B分别以每秒2个单位长度和每秒1个单位长度的速度在数轴上同时相向运动,设运动时间为t秒.
i)是否存在一个常数k,使得3BC-kAB的值在一定时间范围内不随运动时间t的改变而改变?若存在,求出k的值;若不存在,请说明理由.
ii)若点C以每秒3个单位长度的速度向右与点A,B同时运动,何时点C为线段AB的三等分点?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如: 2⊕5=2(2-5)+1=2(-3)+1=-6+1=-5.
(1)求(-2)⊕3的值
(2)若3⊕x的值小于13,求x的取值范围,并在图示的数轴上表示出来.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
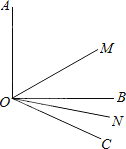
【题目】如图所示,已知∠AOB=90°,∠BOC=20°,OM平分∠AOC,ON平分∠BOC;
(1)求∠MON;
(2)∠AOB=α,∠BOC=β,求∠MON的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com