
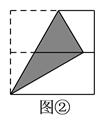
【题目】如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形(阴影部分),且它的一条直角边等于斜边的一半,这样的图形有( ).



A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
【答案】C
【解析】
试题根据含30°角所对的直角边等于斜边一半,然后依次判断直角三角形中能否找到一个角等于30°,从而判断出答案.
试题解析:设正方形的边长为a,
在图①中,CE=ED=![]() a,BC=DB=a,
a,BC=DB=a,
故∠EBC=∠CEB≠30°,故△ECB,故不能满足它的一条直角边等于斜边的一半.
在图②中,BC=![]() a,AC=AE=a,
a,AC=AE=a,
故∠BAC=30°,
从而可得∠CAD=∠EAD=30°,故能满足它的一条直角边等于斜边的一半.
在图③中,AC=![]() a,AB=a,
a,AB=a,
故∠ABC=∠DBC≠30°,故不能满足它的一条直角边等于斜边的一半.
在图④中,AE=![]() a,AB=AD=
a,AB=AD=![]() a,
a,
故∠ABE=30°,∠EAB=60°,
从而可得∠BAC=∠DAC=60°,∠ACB=30°,故能满足它的一条直角边等于斜边的一半.
综上可得有2个满足条件.
故选C.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,射线AM∥BN,点E,F,D在射线AM上,点C在射线BN上,且∠BCD=∠A,BE平分∠ABF,BD平分∠FBC.
(1)求证:AB∥CD.
(2)如果平行移动CD,那么∠AFB与∠ADB的比值是否发生变化?若变化,找出变化规律;若不变,求出这两个角的比值.
(3)如果∠A=100°,那么在平行移动CD的过程中,是否存在某一时刻,使∠AEB=∠BDC?若存在,求出此时∠AEB的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角板的直角顶点C按如图方式叠放在一起,友情提示:∠A=60°,∠D=30°,∠E=∠B=45°.
(1)①若∠DCB=45°,则∠ACB的度数为 .
②若∠ACB=140°,则∠DCE的度数为 .
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<90°且点E在直线AC的上方时,当这两块三角尺有一组边互相平行时,请直接写出∠ACE角度所有可能的值(不必说明理由).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣1,1)、B(4,6)在抛物线y=ax2+bx上
(1)求抛物线的解析式;
(2)如图1,点F的坐标为(0,m)(m>2),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H.设抛物线与x轴的正半轴交于点E,连接FH、AE,求证:FH∥AE;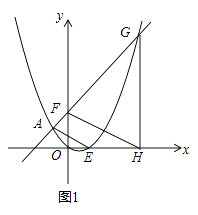
(3)如图2,直线AB分别交x轴、y轴于C、D两点.点P从点C出发,沿射线CD方向匀速运动,速度为每秒 ![]()
个单位长度;同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度.点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=2PM,直接写出t的值.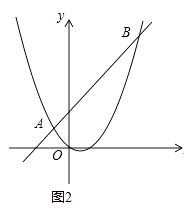
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级(1)班的宣传委员在办黑板报时,采用了下面的图案作为边框,其中每个黑色六边形与6个自色六边形相邻,若一段边框上有25个黑色六边形,则这段边框共有白色六边形

A. 100个 B. 102个 C. 98个 D. 150个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一列数-1,2,-1,2,2,-1,2,2,2,-1,…其中相邻的两个-1被2隔开,第n对-1之问有n个2,则第21个数是______,这一列数的前2019个数的和为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(本小题满分8分)某学校组织八年级学生参加社会实践活动,若单独租用35座客车若干辆,则刚好坐满;若单独租用55座客车,则可以少租一辆,且余45个空座位.
(1)求该校八年级学生参加社会实践活动的人数;
(2)已知35座客车的租金为每辆320元,55座客车的租金为每辆400元.根据租车资金不超过1500元的预算,学校决定同时租用这两种客车共4辆(可以坐不满).请你计算本次社会实践活动所需车辆的租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一列数-1,2,-1,2,2,-1,2,2,2,-1,…其中相邻的两个-1被2隔开,第n对-1之问有n个2,则第21个数是______,这一列数的前2019个数的和为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG交BE于点H,连接DH,下列结论正确的个数是( )
①△ABG∽△FDG ②HD平分∠EHG ③AG⊥BE ④S△HDG:S△HBG=tan∠DAG ⑤线段DH的最小值是2 ![]() ﹣2.
﹣2.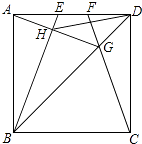
A.2
B.3
C.4
D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com