
【题目】如图,在等腰△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作DE⊥AB,垂足为E.
(1)求证:DE是⊙O的切线.
(2)若DE![]() ,∠C=30°,求
,∠C=30°,求![]() 的长.
的长.
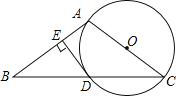
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接OD,只要证明OD⊥DE即可;
(2)连接AD,根据AC是直径,得到∠ADC=90°,利用AB=AC得到BD=CD,解直角三角形求得BD,在Rt△ABD中,解直角三角形求得AD,根据题意证得△AOD是等边三角形,即可OD=AD,然后利用弧长公式求得即可.
(1)证明:连接OD;
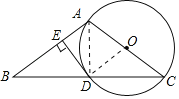
∵OD=OC,
∴∠C=∠ODC,
∵AB=AC,
∴∠B=∠C,
∴∠B=∠ODC,
∴OD∥AB,
∴∠ODE=∠DEB;
∵DE⊥AB,
∴∠DEB=90°,
∴∠ODE=90°,
即DE⊥OD,
∴DE是⊙O的切线.
(2)连接AD,
∵AC是直径,
∴∠ADC=90°,
∵AB=AC,
∴∠B=∠C=30°,BD=CD,
∴∠OAD=60°,
∵OA=OD,
∴△AOD是等边三角形,
∴∠AOD=60°,
∵DE=![]() ,∠B=30°,∠BED=90°,
,∠B=30°,∠BED=90°,
∴CD=BD=2DE=2![]() ,
,
∴OD=AD=tan30°CD![]() ,
,
∴![]() 的长为:
的长为:![]() .
.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】如图, 在等边△ABC中, D, E, F分别为边AB, BC, CA上的点, 且满足∠DEF=60°.
(1)求证:![]() ;
;
(2)若DE⊥BC且DE=EF, 求![]() 的值.
的值.
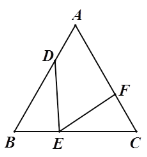
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产一种火爆的网红电子产品,每件产品成本 16 元,工厂将该产品进行网络批发,批发单价 y(元)与一次性批发量 x(件)(x为正整数)之间满 足如图所示的函数关系.
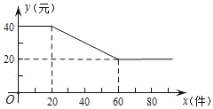
(1)直接写出 y与 x之间所满足的函数关系式,并写出自变量 x的取值范围;
(2)若一次性批发量不低于 20 且不超过 60 件时,求获得的利润 w 与 x 的函数 关系式,同时当批发量为多少件时,工厂获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
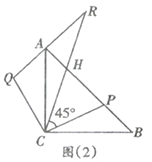
【题目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在斜边
在斜边![]() 上(
上(![]() ),作
),作![]() ,且
,且![]() ,连接
,连接![]() ,如图(1).
,如图(1).
(1)求证:![]() ;
;
(2)延长![]() 至点
至点![]() ,使得
,使得![]() ,
,![]() 与
与![]() 交于点
交于点![]() .如图(2).
.如图(2).
①求证:![]() ;
;
②求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某“综合与实践”小组开展了测量本校旗杆高度的实践活动,他们制订了测量方案,并利用课余时间完成了实地测量.他们在旗杆底部所在的平地上,选取两个不同测点,分别测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差,小组在测量仰角的度数以及两个测点之间的距离时,都分别测量了两次并取它们的平均值作为测量结果,测量数据如下表(不完整)
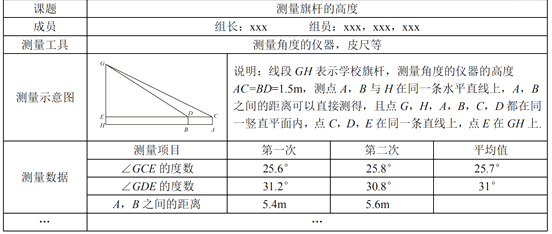

任务一:两次测量A,B之间的距离的平均值是 m.
任务二:根据以上测量结果,请你帮助“综合与实践”小组求出学校学校旗杆GH的高度.
(参考数据:sin25.7°≈0.43,cos25.7°≈0.90,tan25.7°≈0.48,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
任务三:该“综合与实践”小组在定制方案时,讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案,但未被采纳.你认为其原因可能是什么?(写出一条即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容,并按要求解决问题: 问题:“在平面内,已知分别有![]() 个点,
个点,![]() 个点,
个点,![]() 个点,5 个点,…,n 个点,其中任意三 个点都不在同一条直线上.经过每两点画一条直线,它们可以分别画多少条直线? ” 探究:为了解决这个问题,希望小组的同学们设计了如下表格进行探究:(为了方便研 究问题,图中每条线段表示过线段两端点的一条直线)
个点,5 个点,…,n 个点,其中任意三 个点都不在同一条直线上.经过每两点画一条直线,它们可以分别画多少条直线? ” 探究:为了解决这个问题,希望小组的同学们设计了如下表格进行探究:(为了方便研 究问题,图中每条线段表示过线段两端点的一条直线)
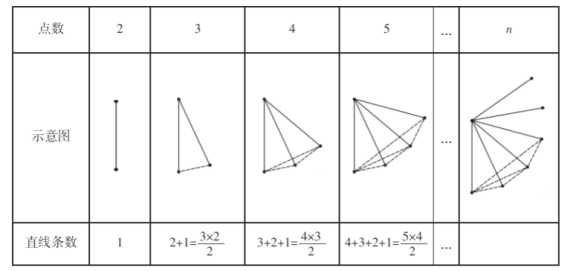
请解答下列问题:
(1)请帮助希望小组归纳,并直接写出结论:当平面内有![]() 个点时,直线条数为 ;
个点时,直线条数为 ;
(2)若某同学按照本题中的方法,共画了![]() 条直线,求该平面内有多少个已知点.
条直线,求该平面内有多少个已知点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内,给定不在同一直线上的点A,B,C,如图所示.点O到点A,B,C的距离均等于a(a为常数),到点O的距离等于a的所有点组成图形G,![]() 的平分线交图形G于点D,连接AD,CD.
的平分线交图形G于点D,连接AD,CD.
(1)求证:AD=CD;
(2)过点D作DE![]() BA,垂足为E,作DF
BA,垂足为E,作DF![]() BC,垂足为F,延长DF交图形G于点M,连接CM.若AD=CM,求直线DE与图形G的公共点个数.
BC,垂足为F,延长DF交图形G于点M,连接CM.若AD=CM,求直线DE与图形G的公共点个数.
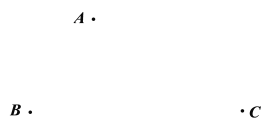
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD与正方形CEFG,点E在CD上,点G在BC的延长线上,M是AF的中点,连接DM,EM.
(1)填空:DM与EM数量关系和位置关系为 (直接填写);
(2)若AB=4,设CE=x(0<x<4),△MEF面积为y,求y关于x的函数关系式[可利用(1)的结论],并求出y的最大值;
(3)如果将正方形CEFG绕点C顺时针旋转任意角度,我们发现DM与EM数量关系与位置关系仍未发生改变.
①若正方形ABCD边长AB=13,正方形CEFG边长CE=5,当D,E,F三点旋转至同一条直线上时,求出MF的长;
②证明结论:正方形CEFG绕点C顺时针旋转任意角度,DM与EM数量关系与位置关系仍未发生改变.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,若二次函数
,若二次函数![]() 的图象过
的图象过![]() 两点,且该函数图象的顶点为
两点,且该函数图象的顶点为![]() ,其中
,其中![]() ,
,![]() 是整数,且
是整数,且![]() ,
,![]() ,则
,则![]() 的值为__________.
的值为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com