
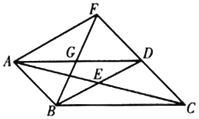
【题目】如图,平行四边形![]() 的对角线
的对角线![]() 与
与![]() 相交于点
相交于点![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)当![]() ,
,![]() 时,请判断四边形
时,请判断四边形![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
(3)当四边形![]() 是正方形时,请判断
是正方形时,请判断![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
【答案】(1)见解析;(2)平行四边形ABDF是矩形,见解理由析;(3)△FBC为等腰直角三角形,证明见解析
【解析】
(1)利用平行四边形的性质,证明AB=CD,然后通过证明△AGB≌△DGF 得出AB=DF即可解决问题;
(2)结论:四边形ABDF是矩形.先证明四边形ABDF是平行四边形,再根据对角线相等的平行四边形是矩形判断即可;
(3)结论:△FBC为等腰直角三角形.由正方形的性质得出∠BFD=45°,∠FGD=90°,根据平行四边形的性质推出BF=BC即可解决问题.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠FDG=∠BAG,
∵点G 是AD的中点,
∴AG=DG,
又∵∠FGD=∠BGA,
∴△AGB≌△DGF(ASA),
∴AB=DF,
∴DF=DC.
(2)结论:四边形ABDF是矩形,
理由:∵△AGB≌△DGF,
∴GF=GB,
又∵DG=AG,
∴四边形ABDF是平行四边形,
∵DG=DC,DC=DF,
∴DF=DG,
在平行四边形ABCD中,
∵∠ABC=120°,
∴∠ADC=120°,
∴∠FDG=60°,
∴△FDG为等边三角形,
∴FG=DG,
∴AD=BF,
∴四边形ABDF是矩形.
(3)当四边形ABDF是正方形时,△FBC为等腰直角三角形.
证明:∵四边形ABDF是正方形,
∴∠BFD=45°,∠FGD=90°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠FBC =∠FGD = 90°,
∴∠FCB = 45°=∠BFD,
∴BF=BC,
∴△FBC为等腰直角三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.

(1)求证:BD平分∠ABC;
(2) 当∠ODB=30°时,求证:BC=OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E、F分别在BC、CD上移动,但A到EF的距离AH始终保持与AB长相等,问在E、F移动过程中:
(1)∠EAF的大小是否有变化?请说明理由.
(2)△ECF的周长是否有变化?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
(发现结论)
(1)如图,在□ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连结B′D,发现两个有趣的结论:①△EAC是等腰三角形 ②AC//B′D 请你选择其中一个结论加以证明
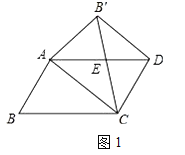
(结论运用)
(2)在□ABCD中,已知:BC=2,∠B=60°,将△ABC沿AC翻折至△AB′C,连结B′D(如上图).若四边形ACDB′是矩形,求AC的长.
(方法拓展)
(3)若 ![]() =k,且以A、C、D、B′为顶点的四边形为正方形,则k的值为 .
=k,且以A、C、D、B′为顶点的四边形为正方形,则k的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委举办了一次“中国梦我的梦”演讲比赛满分10分,学生得分均为整数,成绩达6分以上(含6分)为合格,达到9分以上(含9分)为优秀.如图所示是这次竞赛中甲、乙两组学生成绩分布的条形统计图.
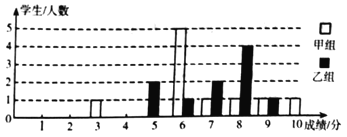
(1)补充完成下列的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲 | 6 | 3.41 | 90% | 20% | |
乙 | 7.1 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是______组学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )

A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种商品,通过记录,发现该商品从开始销售至销售的第x天结束时(x为整数)的总销量y(件)满足二次函数关系,销量情况记录如下表:
x | 0 | 1 | 2 | 3 |
y | 0 | 58 | 112 | 162 |
(1)求y与x之间的函数关系式(不需要写自变量的取值范围);
(2)求:销售到第几天结束时,该商品全部售完?
(3)若第m天的销量为22件,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
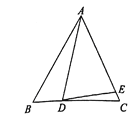
【题目】已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE ,设∠BAD=α,∠CDE=β.
(1)如图,若点D在线段BC上,点E在线段AC上.
①如果∠ABC=60°,∠ADE=70°, 那么α=_______,β=_______.
②求α、β之间的关系式.
(2)是否存在不同于以上②中的α、β之间的关系式?若存在,求出这个关系式,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
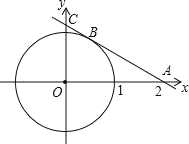
【题目】如图,圆 O 的半径为 1,过点 A(2,0)的直线与圆 O 相切于点 B,与 y 轴相交于点 C.
(1)求 AB 的长;
(2)求直线 AB 的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com