
【题目】如图,点D是⊙O直径CA的延长线上一点,点B在⊙O上,且AB=AD=AO.
(1)求证:BD是⊙O的切线;
(2)若点E是劣弧BC上一点,弦AE与BC相交于点F,且CF=9,cos∠BFA=![]() ,求EF的长.
,求EF的长.
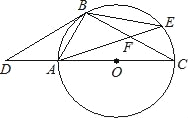
【答案】(1)证明见解析;(2)EF=6.
【解析】分析:(1)连接BO,根据三角形的内角和定理可判断△DOB是直角三角形,则∠OBD=90°,BD是⊙O的切线;
(2)根据圆周角定理,易证△AFB∽△CFE,结合相似比,即可得出EF的长;
详解:(1)证明:连接BO,
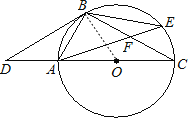
∵AB=AD
∴∠D=∠ABD
∵AB=AO
∴∠ABO=∠AOB
又在△OBD中,∠D+∠DOB+∠ABO+∠ABD=180°
∴∠OBD=90°,即BD⊥BO
∴BD是⊙O的切线;
(2)解:连接CE,
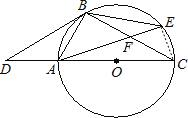
∵AC是直径,
∴∠ABC=∠CEA=90°,
又∵∠AFB=∠CFE,
∴△AFB∽△CFE,
∴![]() ,又CF=9,cos∠BFA=
,又CF=9,cos∠BFA=![]() ,
,
∴EF=![]() ×9=6.
×9=6.


科目:初中数学 来源: 题型:
【题目】如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.
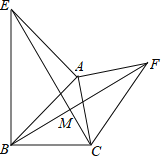
求证:(1)EC=BF;
(2)EC⊥BF;
(3)连接AM,求证:AM平分∠EMF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?请列出二元一次方程组解答此问题.
(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.1.设原来每天安排x名工人生产G型装置,后来补充m名新工人,求x的值(用含m的代数式表示)2.请问至少需要补充多少名新工人才能在规定期内完成总任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC

①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线,将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形;②△HED的面积是1﹣![]() ;③∠AFG=112.5°;④BC+FG=
;③∠AFG=112.5°;④BC+FG=![]() .其中正确的结论是( )
.其中正确的结论是( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴、
与x轴、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,将点
,将点![]() 绕坐标原点
绕坐标原点![]() 顺时针旋转
顺时针旋转![]() 得点
得点![]() ,解答下列问题:
,解答下列问题:
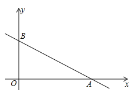
(1)求出点![]() 的坐标,并判断点
的坐标,并判断点![]() 是否在直线l上;
是否在直线l上;
(2)若点![]() 在x轴上,坐标平面内是否存在点
在x轴上,坐标平面内是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,请直接写出
为顶点的四边形是菱形?若存在,请直接写出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
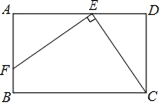
【题目】如图,点E、F分别在矩形ABCD的两条边上,且EF⊥EC,EF=EC,若该矩形的周长为16,AE=3,则DE的长为( )
A. ![]() B. 2 C.
B. 2 C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
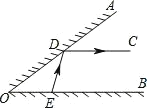
【题目】如图, AOB 的一边 OA 为平面镜, AOB 37°36 ,在 OB 上有一点 E ,从 E 点射出 一束光线经 OA 上一点 D 反射,反射光线 DC 恰好与 OB 平行,则 DEB 的度数是_°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于![]() 的一元二次方程
的一元二次方程![]() 有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,研究发现了此类方程的一般性结论:设其中一根为
有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,研究发现了此类方程的一般性结论:设其中一根为![]() ,则另一根为
,则另一根为![]() ,因此
,因此![]() ,所有有
,所有有![]() ,我们记“
,我们记“![]() ”即
”即![]() ,方程
,方程![]() 为倍根方程,下面我们根据此结论来解决问题:
为倍根方程,下面我们根据此结论来解决问题:
(1)方程①![]() ,方程②
,方程②![]() 这两个方程中,是被根方程的是_____________(填序号即可);
这两个方程中,是被根方程的是_____________(填序号即可);
(2)若![]() 是倍根方程,求
是倍根方程,求![]() 的值;
的值;
(3)若关于![]() 的一元二次方程
的一元二次方程![]() 是倍根方程,且
是倍根方程,且![]() 在一次函数
在一次函数![]() 的图象上,求此倍根方程的表达式。
的图象上,求此倍根方程的表达式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com