练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

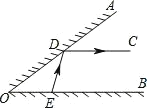
    【题目】如图， AOB 的一边 OA 为平面镜， AOB 37°36 ，在 OB 上有一点 E ，从 E 点射出 一束光线经 OA 上一点 D 反射，反射光线 DC 恰好与 OB 平行，则 DEB 的度数是_°．

    【答案】75.2

    【解析】

    过点D作DF垂直AO交OB于点F,根据题意知,DF是∠CDE的角平分线，故∠1=∠3;然后又由两直线CD∥OB推知内错角∠1=∠2;最后由三角形的内角和定理求得∠DEB的度数.

    解:过点D作DF⊥AO交OB于点F.

    ∵入射角等于反射角

    ∴∠1=∠3

    ∵CD∥OB

    ∴∠1=∠2(两直线平行,内错角相等)

    ∴∠2=∠3(等量代换)

    在Rt△DOF中,∠ODF=90°,∠AOB=37°36′

    ∴∠2=90°-37°36′=52°24′

    ∴在△DEF中，∠DEB=180°-2∠2=75°12′=75.2°

    故答案为75.2.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

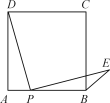
    【题目】点P是正方形ABCD边AB上一点(不与A，B重合)，连接PD并将线段PD绕点P顺时针旋转90°，得线段PE，连接BE，则∠CBE等于( )

    A. 75° B. 60° C. 45° D. 30°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

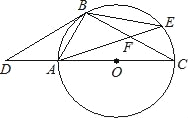
    【题目】如图，点D是⊙O直径CA的延长线上一点，点B在⊙O上，且AB=AD=AO．

    （1）求证：BD是⊙O的切线；

    （2）若点E是劣弧BC上一点，弦AE与BC相交于点F，且CF=9，cos∠BFA=，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：对于给定的一次函数y=ax+b（a≠0），把形如的函数称为一次函数y=ax+b（a≠0）的衍生函数.已知矩形ABCD的顶点坐标分别为A（1，0），B（1，2），C（-3，2），D（-3，0）.

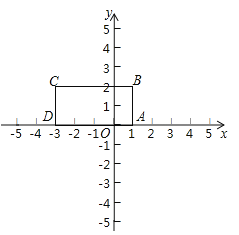
    （1）已知函数y=2x+l.

    ①若点P（-1，m）在这个一次函数的衍生函数图像上，则m= .

    ②这个一次函数的衍生函数图像与矩形ABCD的边的交点坐标分别为 .

    （2）当函数y=kx-3（k>0）的衍生函数的图象与矩形ABCD有2个交点时，k的取值范围是 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线l经过⊙O的圆心O，且与⊙O交于A、B两点，点C在⊙O上，且∠AOC＝30°，点P是直线l上的一个动点(与圆心O不重合)，直线CP与⊙O相交于另一点Q，如果QP＝QO，则∠OCP＝ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们知道，对于一个图形通过不同的方法计算图形的面积，可以得到一个数学等式，例如由图 1 可以得到 (a 2b)(a b) a 3ab 2b，请解答下列问题：

    （1）写出图 2 所表示的数学等式： 　　　　　；

    （2）已知 a b c 12 ，ab bc ac 40 ，利用（1）中所得结论．求abc的值；

    （3）图 3 中给出了若干个边长为 a 和边长为 b 的小正方形纸片、若干个长为 b 宽为 a 的长方 形纸片，选用这些纸片拼出一个图形，使得它的面积是 2a 7ab 3b ．画出该图形，并利用该图形把多项式 2a 7ab 3b分解因式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在东西向的绿道上设有一个岗亭，佳佳从岗亭出发以的速度沿绿道巡逻．规定向东巡逻为正，向西巡逻为负，巡逻情况记录（单位：）如下：

    （1）第六次巡逻结束时，佳佳在岗亭的哪一边？

    （2）在第几次巡逻结束时，佳佳离岗亭最远？

    （3）佳佳一共巡逻多少时间？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）．下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（，y2）是抛物线上两点，则y1＞y2．

    其中说法正确的是（　　）

    A. ①② B. ②③ C. ①②④ D. ②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将四张边长各不相同的正方形纸片按如图方式放入矩形ABCD内（相邻纸片之间互不重叠也无缝隙），未被四张正方形纸片覆盖的部分用阴影表示，设右上角与左下角阴影部分的周长的差为l．若知道l的值，则不需要测量就能知道周长的正方形的标号为（ ）

    A.①B.②C.③D.④

    查看答案和解析>>

    同步练习册答案