
【题目】点P是正方形ABCD边AB上一点(不与A,B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于( )
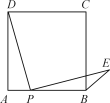
A. 75° B. 60° C. 45° D. 30°
【答案】C
【解析】
过E作AB的延长线AF的垂线,垂足为F,可得出∠F为直角,先利用AAS证明△ADP≌△PEF,根据全等三角形的对应边相等可得出AD=PF,AP=EF,再由正方形的边长相等得到AD=AB,由AP+PB=PB+BF,得到AP=BF,等量代换可得出EF=BF,即三角形BEF为等腰直角三角形,可得出∠EBF为45°,再由∠CBF为直角,即可求出∠CBE的度数.
过点E作EF⊥AF,交AB的延长线于点F,则∠F=90°,
∵四边形ABCD为正方形,
∴AD=AB,∠A=∠ABC=90°,
∴∠ADP+∠APD=90°,
由旋转可得:PD=PE,∠DPE=90°,
∴∠APD+∠EPF=90°,
∴∠ADP=∠EPF,
在△APD和△FEP中
∠ADP=∠FPE
∠A=∠F=90°
PD=EP,
∴△APD≌△FEP(AAS),
∴AP=EF,AD=PF,
又∵AD=AB,
∴PF=AB,即AP+PB=PB+BF,
∴AP=BF,
∴BF=EF,又∠F=91°,
∴△BEF为等腰直角三角形,
∴∠EBF=45°,又∠CBF=91°,
则∠CBE=45°.
故选C.


科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如右图所示,图象过点(-1,0),对称轴为直线x=2,系列结论:(1)4a+b=0;(2)4a+c>2b;(3)5a+3c>0;(4)若点A(-2,y1),点B(,y2),点C(,y3)在该函数图象上,则y1<y3<y2;其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.
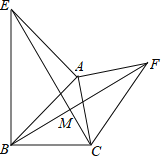
求证:(1)EC=BF;
(2)EC⊥BF;
(3)连接AM,求证:AM平分∠EMF.
查看答案和解析>>
科目:初中数学 来源: 题型:
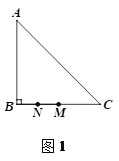
【题目】在△ABC中,∠ABC=90°,AB=BC=4,点M是线段BC的中点,点N在射线MB上,连接AN,平移△ABN,使点N移动到点M,得到△DEM(点D与点A对应,点E与点B对应),DM交AC于点P.
(1)若点N是线段MB的中点,如图1.
① 依题意补全图1;
② 求DP的长;
(2)若点N在线段MB的延长线上,射线DM与射线AB交于点Q,若MQ=DP,求CE的长.
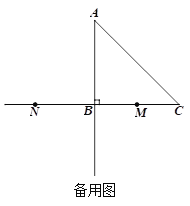
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数![]() 的图象如图所示,则结论:①两函数图象的交点
的图象如图所示,则结论:①两函数图象的交点![]() 的坐标为(2,2);②当x>2时,
的坐标为(2,2);②当x>2时,![]() ;③当x=1时,BC=3;④当x逐渐增大时,
;③当x=1时,BC=3;④当x逐渐增大时,![]() 随着
随着![]() 的增大而增大,
的增大而增大,![]() 随着
随着![]() 的增大而减小.则其中正确结论的序号是( )
的增大而减小.则其中正确结论的序号是( )
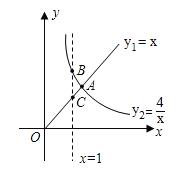
A.①②B.①③C.②④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?请列出二元一次方程组解答此问题.
(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.1.设原来每天安排x名工人生产G型装置,后来补充m名新工人,求x的值(用含m的代数式表示)2.请问至少需要补充多少名新工人才能在规定期内完成总任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC

①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, AOB 的一边 OA 为平面镜, AOB 37°36 ,在 OB 上有一点 E ,从 E 点射出 一束光线经 OA 上一点 D 反射,反射光线 DC 恰好与 OB 平行,则 DEB 的度数是_°.
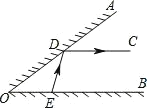
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com