
【题目】在△ABC中,∠ABC=90°,AB=BC=4,点M是线段BC的中点,点N在射线MB上,连接AN,平移△ABN,使点N移动到点M,得到△DEM(点D与点A对应,点E与点B对应),DM交AC于点P.
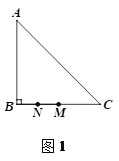
(1)若点N是线段MB的中点,如图1.
① 依题意补全图1;
② 求DP的长;
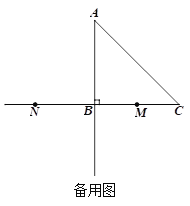
(2)若点N在线段MB的延长线上,射线DM与射线AB交于点Q,若MQ=DP,求CE的长.
【答案】(1)![]() (2)
(2)![]()
【解析】分析:(1)①根据题意补充图形即可;
②连接AD.在Rt△ABN中,由勾股定理得AN的长.由平移的性质得到DM=AN,
进而得到△ADP∽△CMP,由相似三角形的性质即可得到结论.
(2)连接![]() ,先证四边形
,先证四边形![]() 是平行四边形.由平行四边形的性质得到
是平行四边形.由平行四边形的性质得到![]() ∥
∥![]() ,再由平行线的性质得到
,再由平行线的性质得到![]() .进而得到
.进而得到![]() .由平行线分线段成比例定理得到
.由平行线分线段成比例定理得到![]() .由此得到NB的长,即可得到结论.
.由此得到NB的长,即可得到结论.
详解:(1)①如图1,补全图形.
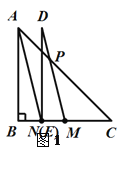
② 连接AD,如图2.
在Rt△ABN中,∵∠B=90°,AB=4,BN=1,∴![]() .
.
∵线段AN平移得到线段DM,∴DM=AN=![]() ,AD=NM=1,AD∥MC,
,AD=NM=1,AD∥MC,
∴△ADP∽△CMP.
∴![]() .
.
∴![]() .
.

(2)连接![]() ,如图3.
,如图3.
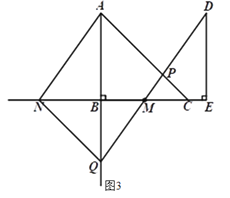
由平移知:![]() ∥
∥![]() ,且
,且![]() =
=![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ∥
∥![]() ,且
,且![]() =
=![]() .
.
∴四边形![]() 是平行四边形.
是平行四边形.
∴![]() ∥
∥![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∵![]() ∥
∥![]() ,
,
∴![]() .
.
又∵![]() 是
是![]() 的中点,且
的中点,且![]() ,
,
∴![]() .
.
∴![]() (舍去负数).
(舍去负数).
∴![]() .
.
∴![]() .
.
方法二,连接AD,如图4.

设CE长为x.
∵线段AB移动到得到线段DE,
∴![]() ,AD∥BM.
,AD∥BM.
∴△ADP∽△CMP.
∴![]() .
.
∵MQ=DP,
∴![]() .
.
∵△QBM∽△QAD,
∴![]() .
.
解得:![]() .
.
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB是一钢架,∠AOB=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH…添的钢管长度都与OE相等,则最多能添加这样的钢管( )根.

A. 2 B. 4 C. 5 D. 无数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市为加快美丽乡村建设,建设秀美幸福宿州,对A、B两类村庄进行了全面改建.根据预算,建设一个A类美丽村庄和一个B类美丽村庄共需资金300万元;甲镇建设了2个A类村庄和5个B类村庄共投入资金1140万元.
(1)建设一个A类美丽村庄和一个B类美丽村庄所需的资金分别是多少万元?
(2)乙镇3个A类美丽村庄和6个B类村庄改建共需资金多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
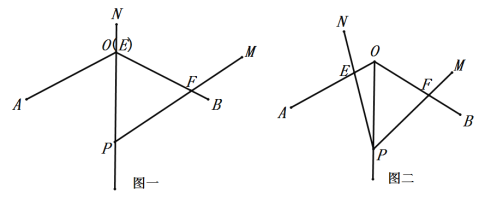
【题目】如图,一伞状图形,已知![]() ,点
,点![]() 是
是![]() 角平分线上一点,且
角平分线上一点,且![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
(1)如图一,当![]() 与
与![]() 重合时,探索
重合时,探索![]() ,
,![]() 的数量关系
的数量关系
(2)如图二,将![]() 在(1)的情形下绕点
在(1)的情形下绕点![]() 逆时针旋转
逆时针旋转![]() 度
度![]() ,继续探索
,继续探索![]() ,
,![]() 的数量关系,并求四边形
的数量关系,并求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
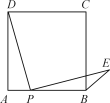
【题目】点P是正方形ABCD边AB上一点(不与A,B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于( )
A. 75° B. 60° C. 45° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,对角线AC、BD交于O点,DE∥AC,CE∥BD.
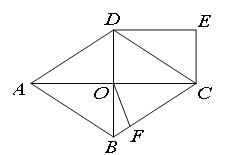
(1)求证:四边形OCED为矩形;
(2)在BC上截取CF=CO,连接OF,若AC=16,BD=12,求四边形OFCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于给定的一次函数y=ax+b(a≠0),把形如![]() 的函数称为一次函数y=ax+b(a≠0)的衍生函数.已知矩形ABCD的顶点坐标分别为A(1,0),B(1,2),C(-3,2),D(-3,0).
的函数称为一次函数y=ax+b(a≠0)的衍生函数.已知矩形ABCD的顶点坐标分别为A(1,0),B(1,2),C(-3,2),D(-3,0).
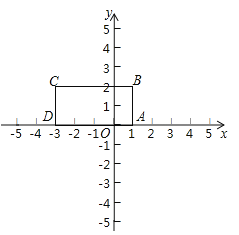
(1)已知函数y=2x+l.
①若点P(-1,m)在这个一次函数的衍生函数图像上,则m= .
②这个一次函数的衍生函数图像与矩形ABCD的边的交点坐标分别为 .
(2)当函数y=kx-3(k>0)的衍生函数的图象与矩形ABCD有2个交点时,k的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com