
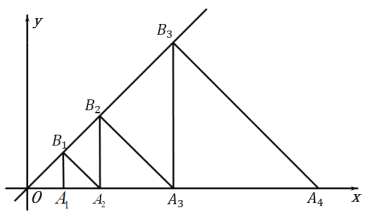
【题目】如图,![]() ,
,![]() ,
,![]() ,…,
,…,![]() 都是等腰直角三角形,其中点
都是等腰直角三角形,其中点![]() ,
,![]() ,…,
,…,![]() 在
在![]() 轴上,点
轴上,点![]() ,
,![]() ,…,
,…,![]() 在直线
在直线![]() 上,已知
上,已知![]() ,则
,则![]() 的长为______________.
的长为______________. ![]()
科目:初中数学 来源: 题型:
【题目】铜梁永辉商场今年二月份以每桶40元的单价购进1000桶甲、乙两种食用油,然后以甲种食用油每桶75元、乙桶食用油每桶60元的价格售完,共获利29000元.
(1)求该商场分别购进甲、乙两种食用油多少桶?
(2)为了增加销售量,获得最大利润,根据销售情况和市场分析,在进价不变的情况下该经销商决定调整价格,将甲种食用油的价格在二月份的基础上下调20%,乙种食用油的价格上涨![]() a%,但甲的销售量还是较二月下降了
a%,但甲的销售量还是较二月下降了![]() a%,而乙的销售量却上升了25%,结果三月份的销售额比二月份增加了1000元,求a的值.
a%,而乙的销售量却上升了25%,结果三月份的销售额比二月份增加了1000元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数 y=kx+b 的图像与反比例函数 y=![]() 的图像交于 A(-2,1),B(1,n)两点,
的图像交于 A(-2,1),B(1,n)两点,
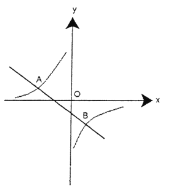
(1)求反比例函数和一次函数的表达式;
(2)求使一次函数的值大于反比例函数的值时 x 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 边上的高,连接
边上的高,连接![]() ,过点
,过点![]() 作
作![]() 与点
与点![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() ,
,![]() .
.
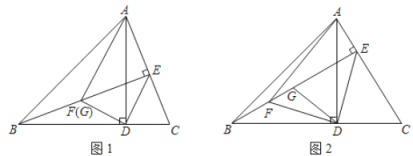
(1)如图![]() ,若点
,若点![]() 与点
与点![]() 重合,求证:
重合,求证:![]() ;
;
(2)如图![]() ,请写出
,请写出![]() 与
与![]() 之间的关系并证明.
之间的关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.
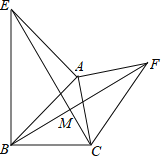
求证:(1)EC=BF;
(2)EC⊥BF;
(3)连接AM,求证:AM平分∠EMF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
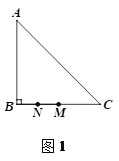
【题目】在△ABC中,∠ABC=90°,AB=BC=4,点M是线段BC的中点,点N在射线MB上,连接AN,平移△ABN,使点N移动到点M,得到△DEM(点D与点A对应,点E与点B对应),DM交AC于点P.
(1)若点N是线段MB的中点,如图1.
① 依题意补全图1;
② 求DP的长;
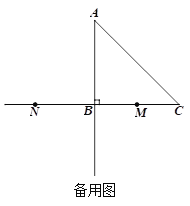
(2)若点N在线段MB的延长线上,射线DM与射线AB交于点Q,若MQ=DP,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
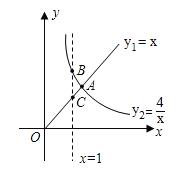
【题目】函数![]() 的图象如图所示,则结论:①两函数图象的交点
的图象如图所示,则结论:①两函数图象的交点![]() 的坐标为(2,2);②当x>2时,
的坐标为(2,2);②当x>2时,![]() ;③当x=1时,BC=3;④当x逐渐增大时,
;③当x=1时,BC=3;④当x逐渐增大时,![]() 随着
随着![]() 的增大而增大,
的增大而增大,![]() 随着
随着![]() 的增大而减小.则其中正确结论的序号是( )
的增大而减小.则其中正确结论的序号是( )
A.①②B.①③C.②④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
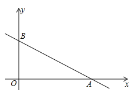
【题目】如图,在平面直角坐标系中,直线![]() 与x轴、
与x轴、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,将点
,将点![]() 绕坐标原点
绕坐标原点![]() 顺时针旋转
顺时针旋转![]() 得点
得点![]() ,解答下列问题:
,解答下列问题:
(1)求出点![]() 的坐标,并判断点
的坐标,并判断点![]() 是否在直线l上;
是否在直线l上;
(2)若点![]() 在x轴上,坐标平面内是否存在点
在x轴上,坐标平面内是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,请直接写出
为顶点的四边形是菱形?若存在,请直接写出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com