【题目】已知多项式
能被
整除，求
的值.
【答案】-2.
【解析】
由多项式2x4-3x3+ax2+7x+b能被x2+x-2整除，得到2x4-3x3+ax2+7x+b=A（x2+x-2）=A（x-1）（x+2），把x=1与x=-2代入，使其值为0列出关于a与b的方程组，求出方程组的解得到a与b的值，即可求出原式的值．
∵多项式2x4-3x3+ax2+7x+b能被x2+x-2=（x-1）（x+2）整除，
∴2x4-3x3+ax2+7x+b=A（x2+x-2）=A（x-1）（x+2），
当x=1时，多项式为2-3+a+7+b=0，即a+b=-6；
当x=-2时，多项式为32+24+4a-14+b=0，即4a+b=-42，
解得：a=-12，b=6，
则
．
科目：初中数学 来源： 题型：
【题目】如图,在平行四边形ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N.给出下列结论：①△ABM≌△CDN；②AM=
AC；③DN=2NF；④S△AMB=
△ABC；其中正确的结论是______________(只填序号)。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知点A（﹣4，4），一个以A为顶点的45°角绕点A旋转，角的两边分别交x轴正半轴，y轴负半轴于E、F，连接EF．当△AEF是直角三角形时，点E的坐标是_____
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我市为加快美丽乡村建设，建设秀美幸福宿州，对A、B两类村庄进行了全面改建．根据预算，建设一个A类美丽村庄和一个B类美丽村庄共需资金300万元；甲镇建设了2个A类村庄和5个B类村庄共投入资金1140万元．
（1）建设一个A类美丽村庄和一个B类美丽村庄所需的资金分别是多少万元？
（2）乙镇3个A类美丽村庄和6个B类村庄改建共需资金多少万元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，过点B（6，0）的直线AB与直线OA相交于点A（4，2），动点M在线段OA和射线AC上运动．
（1）求直线AB的解析式．
（2）求△OAC的面积．
（3）是否存在点M，使△OMC的面积是△OAC的面积的
？若存在求出此时点M的坐标；若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】点P是正方形ABCD边AB上一点(不与A，B重合)，连接PD并将线段PD绕点P顺时针旋转90°，得线段PE，连接BE，则∠CBE等于( )
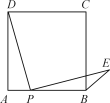
A. 75° B. 60° C. 45° D. 30°
查看答案和解析>>
科目：初中数学 来源： 题型：
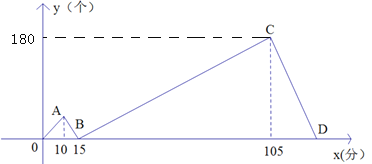
【题目】甲，乙两人同时各接受了600个零件的加工任务，甲比乙每分钟加工的数量多，两人同时开始加工，加工过程中其中一人因故障停止加工几分钟后又继续按原速加工，直到他们完成任务，如图表示甲比乙多加工的零件数量
（个）与加工时间
（分）之间的函数关系，观察图象解决下列问题：
（1）点B的坐标是________，B点表示的实际意义是___________ _____；
（2）求线段BC对应的函数关系式和D点坐标；
（3）乙在加工的过程中，多少分钟时比甲少加工100个零件？
（4）为了使乙能与甲同时完成任务，现让丙帮乙加工，直到完成.丙每分钟能加工3个零件，并把丙加工的零件数记在乙的名下，问丙应在第多少分钟时开始帮助乙？并在图中用虚线画出丙帮助后y与x之间的函数关系的图象.
查看答案和解析>>
科目：初中数学 来源： 题型：
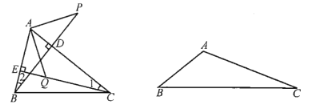
【题目】（1）如图所示，BD，CE是
的高，点P在BD的延长线上，
，点Q在CE上，
，探究PA与AQ之间的关系；
（2）若把（1）中的改为钝角三角形，
，
是钝角，其他条件不变，上述结论是否成立？画出图形并证明你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线l经过⊙O的圆心O，且与⊙O交于A、B两点，点C在⊙O上，且∠AOC＝30°，点P是直线l上的一个动点(与圆心O不重合)，直线CP与⊙O相交于另一点Q，如果QP＝QO，则∠OCP＝ ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com