Question

【题目】如图,在平行四边形ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N.给出下列结论：①△ABM≌△CDN；②AM=AC；③DN=2NF；④S△AMB=△ABC；其中正确的结论是______________(只填序号)。

Answer 1

【答案】①②③.

【解析】

本题先结合平行四边形性质，根据ASA得出△ABM≌△CDN，从而得出DN=BM，AM=CN；再由三角形中位线得出CN=MN，BM=DN=2NF，同时S =S．

∵因为平行四边形ABCD，

∴AD=BC,AB=CD,且AD∥BC，AB∥CD∠BAE=∠DCF，

∵E、F分别是边AD、BC的中点，

∴AE=DE=BF=CF，

∴四边形BFDE是平行四边形

∴BE∥DF，

在△ABE和△CDF中

∵ ，

∴△ABE≌△CDF(SAS)，

∴∠ABM=∠CDN，

∵AB∥CD，

∴∠BAM=∠DCN，

在△ABM和△CDN中

∵ ，

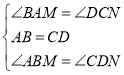∴△ABM≌△CDN(ASA)，∴①正确；

∵E是AD的中点,BE∥DF，

∴M是AN的中点，

同理N是CM的中点，

∴AM=AC，故②正确；

∵F为BC的中点，

∴NF为三角形BCM的中位线，

∴BM=2NF

∴DN=2NF，故③正确；

∵CN=MN=AM，

∴S =S，故④不正确，

∴其中正确的结论是①②③.

故答案为：①②③.