【题目】已知：
、
、
为△ABC的三边长，且
试判定△ABC的形状。
【答案】△ABC为等腰三角形，理由见解析；
【解析】
先把前面两项展开得到a
b-ac+bc-ab+c（a-b）=0，再分组分解，得到公因式（a-b），则ab（a-b）-c（a-b）（a+b）+c（a-b）=0，所以把等式左边分解得到（a-b）（ab-ac-bc+c）=0，接着在把中括号内分组分解得到（a-b）（b-c）（a-c）=0，然后根据有理数积的性质得到a-b=0或b-c=0或a-c=0，于是根据等腰三角形的判定方法进行判断．
△ABC为等腰三角形，理由如下：
∵a (bc)+ b(ca)+c(ab)=0，
∴abac+bcab+c(ab)=0，
∴ab(ab)c(ab)+c(ab)=0，
∴ab(ab)c(ab)(a+b)+c(ab)=0，
∴(ab)(abacbc+c)=0，
∴(ab)[a(bc)c(bc)]=0，
∴(ab)(bc)(ac)=0，
∴ab=0或bc=0或ac=0，
∴△ABC为等腰三角形.
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC和△ADE都是等腰直角三角形，∠ACB=∠ADE=90°，点F为BE的中点，连接CF，DF．
（1）如图1，当点D在AB上，点E在AC上时
①证明：△BFC是等腰三角形；
②请判断线段CF，DF的关系？并说明理由；
（2）如图2，将图1中的△ADE绕点A旋转到图2位置时，请判断（1）中②的结论是否仍然成立？并证明你的判断．
查看答案和解析>>
科目：初中数学 来源： 题型：
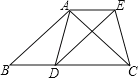
【题目】已知：如图，在△ABC中，AB=AC，D为边BC上一点，以AB，BD为邻边作平行四边形ABDE，连接AD，EC．
（1）求证：AD=CE；
（2）当点D在什么位置时，四边形ADCE是矩形，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为了准备“迎新活动”，用700元购买了甲、乙两种小礼品260个，其中购买甲种礼品比乙种礼品少用了100元．
（1）购买乙种礼品花了______元；
（2）如果甲种礼品的单价比乙种礼品的单价高20%，求乙种礼品的单价．（列分式方程解应用题）
查看答案和解析>>
科目：初中数学 来源： 题型：
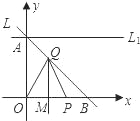
【题目】如图所示，已知直线L过点A（0，1）和B（1，0），P是x轴正半轴上的动点，OP的垂直平分线交L于点Q，交x轴于点M．
（1）直接写出直线L的解析式；
（2）设OP＝t，△OPQ的面积为S，求S关于t的函数关系式；并求出当0＜t＜2时，S的最大值；
（3）直线L1过点A且与x轴平行，问在L1上是否存在点C，使得△CPQ是以Q为直角顶点的等腰直角三角形？若存在，求出点C的坐标，并证明；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，EF⊥AC于点F，DB⊥AC于点M，∠1=∠2，∠3=∠C，请问AB与MN平行吗？说明理由．完成下列推理过程：
解：AB∥MN．理由如下：
∵EF⊥AC，DB⊥AC，（已知），
∴∠CFE=∠CMD=90°，（ ）
∴EF∥DM，（ ）
∴∠2=∠CDM，（ ）
∵∠1=∠2，（已知），
∴∠1=∠ （ ）
∴MN∥CD，（ ）
∵∠3=∠C，（已知），
∴AB∥CD，（ ），
∴AB∥MN．（ ）
查看答案和解析>>
科目：初中数学 来源： 题型：
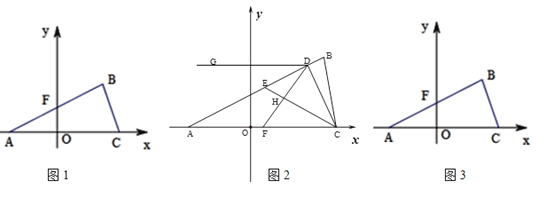
【题目】如图1，在平面直角坐标系中，点A（a，0），B（b，3），C（c，0），满足
+
+
=0．
（1）分别求出点
，
，
的坐标及三角形ABC的面积．
（2）如图2．过点C作
于点D，F是线段AC上一点，满足
，若点G是第二象限内的一点，连接DG，使
，点E是线段AD上一动点（不与A、D重合），连接CE交DF于点H，点E在线段AD上运动的过程中，
的值是否会变化？若不变，请求出它的值；若变化，请说明理由．
（3）如图3，若线段AB与
轴相交于点F，且点F的坐标为（0，
），在坐标轴上是否存在一点P，使三角形ABP和三角形ABC的面积相等？若存在，求出P点坐标．若不存在，请说明理由．（点C除外）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,在平行四边形ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N.给出下列结论：①△ABM≌△CDN；②AM=
AC；③DN=2NF；④S△AMB=
△ABC；其中正确的结论是______________(只填序号)。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知点A（﹣4，4），一个以A为顶点的45°角绕点A旋转，角的两边分别交x轴正半轴，y轴负半轴于E、F，连接EF．当△AEF是直角三角形时，点E的坐标是_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com