
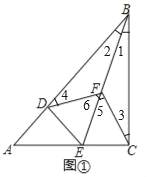
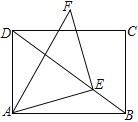
【题目】如图,已知△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE的中点,连接CF,DF.

(1)如图1,当点D在AB上,点E在AC上时
①证明:△BFC是等腰三角形;
②请判断线段CF,DF的关系?并说明理由;
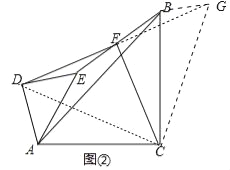
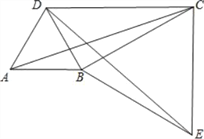
(2)如图2,将图1中的△ADE绕点A旋转到图2位置时,请判断(1)中②的结论是否仍然成立?并证明你的判断.
【答案】(1)①证明见解析;②结论:CF=DF且CF⊥DF.理由见解析;(2)(1)中的结论仍然成立.理由见解析.
【解析】分析:(1)、根据“直角三角形斜边上的中线等于斜边的一半”可知CF=BF=EF,根据∠CFD=2∠ABC,∠ACB=90°,∠ABC=45°得出∠CFD=90°,从而得出答案;(2)、延长DF至G使FG=DF,连接BG,CG,DC,首先证明△BFG和△EFD全等,然后再证明△BCG和△ACD全等,从而得出GC=DC,∠BCG=∠ACD,∠DCG=∠ACB=90°,最后根据直角三角形斜中线的性质得出答案.
详解:(1)①证明:∵∠BCE=90°.EF=FB,∴CF=BF=EF,∴△BFC是等腰三角形.
②解:结论:CF=DF且CF⊥DF.理由如下:
∵∠ADE=90°,∴∠BDE=90°,又∵∠BCE=90°,点F是BE的中点,∴CF=DF=![]() BE=BF,
BE=BF,
∴∠1=∠3,∠2=∠4,∴∠5=∠1+∠3=2∠1,∠6=∠2+∠4=2∠2,
∴∠CFD=∠5+∠6=2(∠1+∠2)=2∠ABC,
又∵△ABC是等腰直角三角形,且∠ACB=90°,∴∠ABC=45°,∴∠CFD=90°,
∴CF=DF且CF⊥DF.
(2)(1)中的结论仍然成立.理由如下:
如图,延长DF至G使FG=DF,连接BG,CG,DC,∵F是BE的中点,∴BF=EF,
又∵∠BFG=∠EFD,GF=DF,∴△BFG≌△EFD(SAS),∴∠FBG=∠FED,BG=ED,
∴BG∥DE,∵△ADE和△ACB都是等腰直角三角形,
∴DE=DA,∠DAE=∠DEA=45°,AC=BC,∠CAB=∠CBA=45°,
又∵∠CBG=∠EBG﹣∠EBA﹣∠ABC=∠DEF﹣(180°﹣∠AEB﹣∠EAB)﹣45°
=∠DEF﹣180°+∠AEB+∠EAB﹣45°=(∠DEF+∠AEB)+∠EAB﹣225°
=360°﹣∠DEA+∠EAB﹣225°=360°﹣45°+∠EAB﹣225°=90°+∠EAB,
而∠DAC=∠DAE+∠EAB+∠CAB=45°+∠EAB+45°=90°+∠EAB,
∴∠CBG=∠DAC,又∵BG=ED,DE=DA,∴BG=AD,又∵BC=AC,
∴△BCG≌△ACD(SAS),∴GC=DC,∠BCG=∠ACD,
∴∠DCG=∠DCB+∠BCG=∠DCB+∠ACD=∠ACB=90°,
∴△DCG是等腰直角三角形,又∵F是DG的中点,∴CF⊥DF且CF=DF.


科目:初中数学 来源: 题型:
【题目】目前节能灯在城市已基本普及,某商场计划购进甲、乙两种节能订共1200只,这两种节能灯的进价、售价如下表:
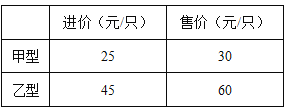
(1)如何进货,进货款恰好为46000元?
(2)为确保乙型节能灯顺利畅销,在(1)的条件下,商家决定对乙型节能灯进行打折出售,且全部售完后,乙型节能灯的利润率为20%,请同乙型节能灯需打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“金牛绿道行“活动需要租用![]() 、
、![]() 两种型号的展台,经前期市场调查发现,用
两种型号的展台,经前期市场调查发现,用![]() 元租用的
元租用的![]() 型展台的数量与用
型展台的数量与用![]() 元租用的
元租用的![]() 型展台的数量相同,且每个
型展台的数量相同,且每个![]() 型展台的价格比每个
型展台的价格比每个![]() 型展台的价格少
型展台的价格少![]() 元.
元.
(1)求每个![]() 型展台、每个
型展台、每个![]() 型展台的租用价格分别为多少元(列方程解应用题);
型展台的租用价格分别为多少元(列方程解应用题);
(2)现预计投入资金至多![]() 元,根据场地需求估计,
元,根据场地需求估计,![]() 型展台必须比
型展台必须比![]() 型展台多
型展台多![]() 个,问
个,问![]() 型展台最多可租用多少个.
型展台最多可租用多少个.
查看答案和解析>>
科目:初中数学 来源: 题型:
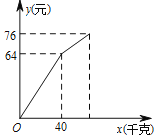
【题目】小明在暑期社会实践活动中,以每千克0.8元的价格从批发市场购进若干千克瓜到市场上去销售,销售了40kg西瓜之后,余下的每千克降价0.4元,全部售完销售金额与售出西瓜的千克数之间的关系如图所示,小明这次卖瓜赚________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,AD=3,E为对角线BD上一个动点,以E为直角顶点,AE为直角边作等腰Rt△AEF,A、E、F按逆时针排列.当点E从点B运动到点D时,点F的运动路径长为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
(1)以下四边形中,是勾股四边形的为 .(填写序号即可)
①矩形;②有一个角为直角的任意凸四边形;③有一个角为60°的菱形.
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,∠DCB=30°,连接AD,DC,CE.
①求证:△BCE是等边三角形;
②求证:四边形ABCD是勾股四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(﹣3,4),B(﹣4,2),C(﹣2,1),△ABC绕原点逆时针旋转90°,得到△A1B1C1,将△A1B1C1向右平移6个单位,再向上平移2个单位得到△A2B2C2.
(1)画出△A1B1C1和△A2B2C2;
(2)△ABC经旋转、平移后点A的对应点分别为A1、A2,请写出点A1、A2的坐标;
(3)P(a,b)是△ABC的边AC上一点,△ABC经旋转、平移后点P的对应点分别为P1,P2,请写出点P1、P2的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com