
【题目】在东西向的绿道上设有一个岗亭,佳佳从岗亭出发以![]() 的速度沿绿道巡逻.规定向东巡逻为正,向西巡逻为负,巡逻情况记录(单位:
的速度沿绿道巡逻.规定向东巡逻为正,向西巡逻为负,巡逻情况记录(单位:![]() )如下:
)如下:
![]()
(1)第六次巡逻结束时,佳佳在岗亭的哪一边?
(2)在第几次巡逻结束时,佳佳离岗亭最远?
(3)佳佳一共巡逻多少时间?
【答案】(1)第六次巡逻结束时,佳佳在岗亭的东边;(2)在第五次巡逻结束时,佳佳离岗亭最远;(3)佳佳一共巡逻2h.
【解析】
(1)根据表格中正负数的意义和有理数的加法法则计算出结果即可判断;
(2)分析出每一次巡逻结束时,佳佳到岗亭的距离,然后比较大小即可得出结论;
(3)先求出佳佳巡逻的总路程,然后根据时间=路程÷速度,计算即可.
解:(1)![]() ,
,
∵1>0
∴第六次巡逻结束时,佳佳在岗亭的东边
答:第六次巡逻结束时,佳佳在岗亭的东边.
(2)第一次距离岗亭![]() ;
;
第二次距离岗亭![]() ;
;
第三次距离岗亭![]() ;
;
第四次距离岗亭![]() ;
;
第五次距离岗亭![]() ;
;
第六次距离岗亭![]() ;
;
第七次距离岗亭![]() .
.
∵5>4>2>1>0
答:在第五次巡逻结束时,佳佳离岗亭最远.
(3)佳佳巡逻的总路程为:![]() ,
,
∴巡逻时间为:![]() .
.
答:佳佳一共巡逻2h.


科目:初中数学 来源: 题型:
【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?请列出二元一次方程组解答此问题.
(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.1.设原来每天安排x名工人生产G型装置,后来补充m名新工人,求x的值(用含m的代数式表示)2.请问至少需要补充多少名新工人才能在规定期内完成总任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F分别在矩形ABCD的两条边上,且EF⊥EC,EF=EC,若该矩形的周长为16,AE=3,则DE的长为( )
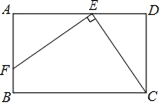
A. ![]() B. 2 C.
B. 2 C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
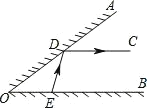
【题目】如图, AOB 的一边 OA 为平面镜, AOB 37°36 ,在 OB 上有一点 E ,从 E 点射出 一束光线经 OA 上一点 D 反射,反射光线 DC 恰好与 OB 平行,则 DEB 的度数是_°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】原题呈现:若 a ![]() b
b![]() 4a 2b 5 0 ,求 a、b 的值.方法介绍:
4a 2b 5 0 ,求 a、b 的值.方法介绍:
①看到 a ![]() 4a 可想到如果添上常数 4 恰好就是 a
4a 可想到如果添上常数 4 恰好就是 a ![]() 4a 4 (a 2)
4a 4 (a 2)![]() ,这个过程叫做“配方”,同理 b
,这个过程叫做“配方”,同理 b ![]() 2b 1 (b 1)
2b 1 (b 1) ![]() ,恰好把常数5分配完;
,恰好把常数5分配完;
②从而原式可以化为(a 2)![]() (b 1)
(b 1)![]() 0 由平方的非负性可得 a 2 0 且 b 1 0.经验运用:
0 由平方的非负性可得 a 2 0 且 b 1 0.经验运用:
(1)若 4a ![]() b
b![]() 20a 6b 34 0 求 a b 的值;
20a 6b 34 0 求 a b 的值;
(2)若 a![]() 5b
5b![]() c
c ![]() 2ab 4b 6c 10 0 求 a b c 的值.
2ab 4b 6c 10 0 求 a b c 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
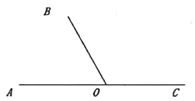
【题目】如图,在平面内,点![]() 是直线
是直线![]() 上一点,
上一点,![]() ,射线
,射线![]() 不动,射线
不动,射线![]() ,
,![]() 同时开始绕点
同时开始绕点![]() 顺时针转动,射线
顺时针转动,射线![]() 首次回到起始位置时两线同时停止转动,射线
首次回到起始位置时两线同时停止转动,射线![]() ,
,![]() 的转动速度分别为每秒
的转动速度分别为每秒![]() 和每秒
和每秒![]() .若转动
.若转动![]() 秒时,射线
秒时,射线![]() ,
,![]() ,
,![]() 中的一条是另外两条组成角的角平分线,则
中的一条是另外两条组成角的角平分线,则![]() ______秒.
______秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于![]() 的一元二次方程
的一元二次方程![]() 有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,研究发现了此类方程的一般性结论:设其中一根为
有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,研究发现了此类方程的一般性结论:设其中一根为![]() ,则另一根为
,则另一根为![]() ,因此
,因此![]() ,所有有
,所有有![]() ,我们记“
,我们记“![]() ”即
”即![]() ,方程
,方程![]() 为倍根方程,下面我们根据此结论来解决问题:
为倍根方程,下面我们根据此结论来解决问题:
(1)方程①![]() ,方程②
,方程②![]() 这两个方程中,是被根方程的是_____________(填序号即可);
这两个方程中,是被根方程的是_____________(填序号即可);
(2)若![]() 是倍根方程,求
是倍根方程,求![]() 的值;
的值;
(3)若关于![]() 的一元二次方程
的一元二次方程![]() 是倍根方程,且
是倍根方程,且![]() 在一次函数
在一次函数![]() 的图象上,求此倍根方程的表达式。
的图象上,求此倍根方程的表达式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com