
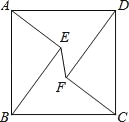
【题目】如图,在正方形ABCD中,AD=5,点E,F是正方形ABCD内的两点,且AE=FC=3,BE=DF=4,则EF的长为_____.
【答案】![]()
【解析】分析:延长AE交DF于G,再根据全等三角形的判定得出△AGD与△ABE全等,得出AG=BE=4,由AE=3,得出EG=1,同理得出GF=1,再根据勾股定理得出EF的长.
详解:延长AE交DF于G,如图, ∵AB=5,AE=3,BE=4,
∴△ABE是直角三角形,
同理可得△DFC是直角三角形,可得△AGD是直角三角形,
∴∠ABE+∠BAE=∠DAE+∠BAE,∴∠GAD=∠EBA,
同理可得:∠ADG=∠BAE.
在△AGD和△BAE中,∵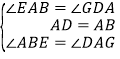 ,
,
∴△AGD≌△BAE(ASA),
∴AG=BE=4,DG=AE=3,∴EG=4﹣3=1,
同理可得:GF=1,∴EF=![]() .
.
故答案为:![]() .
.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】在东西向的绿道上设有一个岗亭,佳佳从岗亭出发以![]() 的速度沿绿道巡逻.规定向东巡逻为正,向西巡逻为负,巡逻情况记录(单位:
的速度沿绿道巡逻.规定向东巡逻为正,向西巡逻为负,巡逻情况记录(单位:![]() )如下:
)如下:
![]()
(1)第六次巡逻结束时,佳佳在岗亭的哪一边?
(2)在第几次巡逻结束时,佳佳离岗亭最远?
(3)佳佳一共巡逻多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
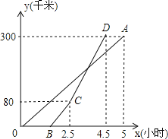
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.当轿车到达乙地后,马上沿原路以CD段速度返回,则货车从甲地出发_______小时后与轿车相遇(结果精确到0.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将四张边长各不相同的正方形纸片按如图方式放入矩形ABCD内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示,设右上角与左下角阴影部分的周长的差为l.若知道l的值,则不需要测量就能知道周长的正方形的标号为( )

A.①B.②C.③D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
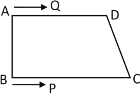
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=8cm,BC=10cm,AB=6cm,点Q从点A出发以1 cm/s的速度向点D运动,点P从点B出发以2 cm/s的速度向点C运动,P,Q两点同时出发,当点P到达点C时,两点同时停止运动.若设运动时间为t(s)
(1)直接写出:QD=______cm,PC=_______cm;(用含t的式子表示)
(2)当t为何值时,四边形PQDC为平行四边形?
(3)若点P与点C不重合,且DQ≠DP,当t为何值时,△DPQ是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=0.5千米,则该沙田的面积为________________平方千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
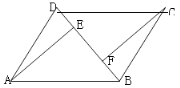
【题目】在![]() 中,BD是它的一条对角线,过A、C两点分别作
中,BD是它的一条对角线,过A、C两点分别作![]() ,
,![]() ,E、F为垂足.
,E、F为垂足.
(1)如图,求证:![]() ;
;
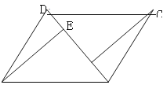
(2)如图,连接AC,设AC、BD交于点O,若![]() .在不添加任何辅助线的情况下,请直接写出图中的所有长度是OE长度2倍的线段.
.在不添加任何辅助线的情况下,请直接写出图中的所有长度是OE长度2倍的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用1 000元购进一批“晨光”套尺,很快销售一空;商店又用1 500元购进第二批该款套尺,购进时单价是第一批的![]() 倍,所购数量比第一批多100套.
倍,所购数量比第一批多100套.
(1)求第一批套尺购进时单价是多少?
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com