
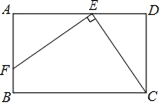
【题目】如图,点E、F分别在矩形ABCD的两条边上,且EF⊥EC,EF=EC,若该矩形的周长为16,AE=3,则DE的长为( )
A. ![]() B. 2 C.
B. 2 C. ![]() D. 3
D. 3
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】我市为加快美丽乡村建设,建设秀美幸福宿州,对A、B两类村庄进行了全面改建.根据预算,建设一个A类美丽村庄和一个B类美丽村庄共需资金300万元;甲镇建设了2个A类村庄和5个B类村庄共投入资金1140万元.
(1)建设一个A类美丽村庄和一个B类美丽村庄所需的资金分别是多少万元?
(2)乙镇3个A类美丽村庄和6个B类村庄改建共需资金多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
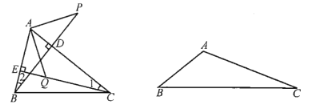
【题目】(1)如图所示,BD,CE是![]() 的高,点P在BD的延长线上,
的高,点P在BD的延长线上,![]() ,点Q在CE上,
,点Q在CE上,![]() ,探究PA与AQ之间的关系;
,探究PA与AQ之间的关系;
(2)若把(1)中的![]() 改为钝角三角形,
改为钝角三角形,![]() ,
,![]() 是钝角,其他条件不变,上述结论是否成立?画出图形并证明你的结论.
是钝角,其他条件不变,上述结论是否成立?画出图形并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
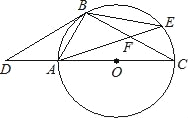
【题目】如图,点D是⊙O直径CA的延长线上一点,点B在⊙O上,且AB=AD=AO.
(1)求证:BD是⊙O的切线;
(2)若点E是劣弧BC上一点,弦AE与BC相交于点F,且CF=9,cos∠BFA=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批彩色弹力球的质量检验结果如下表:
抽取的彩色弹力球数n | 500 | 1000 | 1500 | 2000 | 2500 |
优等品频数m | 471 | 946 | 1426 | 1898 | 2370 |
优等品频率 | 0.942 | 0.946 | 0.951 | 0.949 | 0.948 |
(1)请在图中完成这批彩色弹力球“优等品”频率的折线统计图
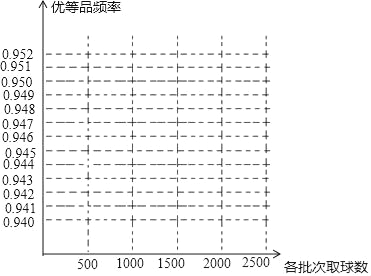
(2)这批彩色弹力球“优等品”概率的估计值大约是多少?(精确到0.01)
(3)从这批彩色弹力球中选择5个黄球、13个黑球、22个红球,它们除了颜色外都相同,将它们放入一个不透明的袋子中,求从袋子中摸出一个球是黄球的概率.
(4)现从第(3)问所说的袋子中取出若干个黑球,并放入相同数量的黄球,搅拌均匀,使从袋子中摸出一个黄球的概率为![]() ,求取出了多少个黑球?
,求取出了多少个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于给定的一次函数y=ax+b(a≠0),把形如![]() 的函数称为一次函数y=ax+b(a≠0)的衍生函数.已知矩形ABCD的顶点坐标分别为A(1,0),B(1,2),C(-3,2),D(-3,0).
的函数称为一次函数y=ax+b(a≠0)的衍生函数.已知矩形ABCD的顶点坐标分别为A(1,0),B(1,2),C(-3,2),D(-3,0).
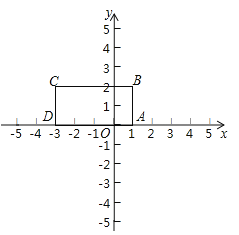
(1)已知函数y=2x+l.
①若点P(-1,m)在这个一次函数的衍生函数图像上,则m= .
②这个一次函数的衍生函数图像与矩形ABCD的边的交点坐标分别为 .
(2)当函数y=kx-3(k>0)的衍生函数的图象与矩形ABCD有2个交点时,k的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l经过⊙O的圆心O,且与⊙O交于A、B两点,点C在⊙O上,且∠AOC=30°,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于另一点Q,如果QP=QO,则∠OCP= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东西向的绿道上设有一个岗亭,佳佳从岗亭出发以![]() 的速度沿绿道巡逻.规定向东巡逻为正,向西巡逻为负,巡逻情况记录(单位:
的速度沿绿道巡逻.规定向东巡逻为正,向西巡逻为负,巡逻情况记录(单位:![]() )如下:
)如下:
![]()
(1)第六次巡逻结束时,佳佳在岗亭的哪一边?
(2)在第几次巡逻结束时,佳佳离岗亭最远?
(3)佳佳一共巡逻多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.当轿车到达乙地后,马上沿原路以CD段速度返回,则货车从甲地出发_______小时后与轿车相遇(结果精确到0.01)
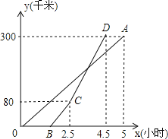
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com