练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】因式分解

    （1） （2）（x+y）2-16（x-y）2

    （3）－2x2y＋12xy－18y （4）a4-8a2b2+16b4 （5）x4-1

    【答案】（1）7x2（x﹣3）；（2）（5x-3y）（5y﹣3x）；（3）；（4）；（5）.

    【解析】

    （1）利用提取公因式法进行因式分解即可；

    （2）利用平方差公式进行因式分解即可；

    （3）先提取公因式，再利用完全平方公式进行因式分解即可；

    （4）先利用完全平方公式，再利用平方差公式进行因式分解即可；

    （5）利用两次平方差公式进行因式分解即可.

    解：（1）原式=7x2（x﹣3）；

    （2）原式=（x+y+4x﹣4y）（x+y﹣4x+4y）=（5x-3y）（5y﹣3x）；

    （3）原式；

    （4）原式；

    （5）原式.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

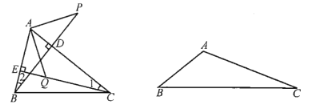
    【题目】（1）如图所示，BD，CE是的高，点P在BD的延长线上，，点Q在CE上，，探究PA与AQ之间的关系；

    （2）若把（1）中的改为钝角三角形，，是钝角，其他条件不变，上述结论是否成立？画出图形并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线l经过⊙O的圆心O，且与⊙O交于A、B两点，点C在⊙O上，且∠AOC＝30°，点P是直线l上的一个动点(与圆心O不重合)，直线CP与⊙O相交于另一点Q，如果QP＝QO，则∠OCP＝ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在东西向的绿道上设有一个岗亭，佳佳从岗亭出发以的速度沿绿道巡逻．规定向东巡逻为正，向西巡逻为负，巡逻情况记录（单位：）如下：

    （1）第六次巡逻结束时，佳佳在岗亭的哪一边？

    （2）在第几次巡逻结束时，佳佳离岗亭最远？

    （3）佳佳一共巡逻多少时间？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们用a表示不大于 a 的最大整数，用 a 表示大于 a 的最小整数.例如：2.5 2 ，3 3 ， 2.5 3 ；<2.5> 3 ，<4> 5 ，< 1.5> 1 .解决下列问题：

    （1） 4.5 ,< 3.5> .

    （2）若x 2 ，则 < x> 的取值范围是 ；若< y > 1，则 y 的取值范围是 .

    （3）已知 x, y 满足方程组；求 x, y 的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）．下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（，y2）是抛物线上两点，则y1＞y2．

    其中说法正确的是（　　）

    A. ①② B. ②③ C. ①②④ D. ②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：

    一般地，在数轴上点，表示的实数分别为，（），则，两点的距离．如图，在数轴上点，表示的实数分别为-3，4，则记，，因为，显然，两点的距离．

    若点为线段的中点，则，所以，即．

    解决问题：

    （1）直接写出线段的中点表示的实数　　　　 ；

    （2）在点右侧的数轴上有点，且，求点表示的实数；

    （3）在（2）的条件下，点是的中点，点是的中点，若，两点同时沿数轴向正方向运动，点的速度是点速度的2倍，的中点和的中点也随之运动，3秒后，，则点的速度为每秒　　　　 个单位长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

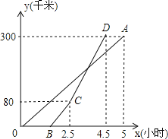
    【题目】甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地，如图，线段OA表示货车离甲地距离y（千米）与时间x（小时）之间的函数关系；折线BCD表示轿车离甲地距离y（千米）与x（小时）之间的函数关系．当轿车到达乙地后，马上沿原路以CD段速度返回，则货车从甲地出发_______小时后与轿车相遇（结果精确到0.01）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

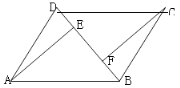
    【题目】在中，BD是它的一条对角线，过A、C两点分别作，，E、F为垂足．

    （1）如图，求证：；

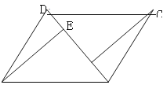
    （2）如图，连接AC，设AC、BD交于点O，若．在不添加任何辅助线的情况下，请直接写出图中的所有长度是OE长度2倍的线段．

    查看答案和解析>>

    同步练习册答案