
分析 以人均捐款数为问题,等量关系为:1班人数×90%=2班人数;
以人数为问题,等量关系为:1班人均捐款数+4=2班人均捐款数.
解答 解:解法一:求两个班人均捐款各多少元?
设1班人均捐款x元,则2班人均捐款(x+4)元.
根据题意得:$\frac{1800}{x}$×(1-10%)=$\frac{1800}{x+4}$,
解得:x=36,
经检验x=36是原方程的根.
则x+4=40,
答:1班人均捐36元,2班人均捐40元.
解法二:求两个班人数各多少人?
设1班有x人,则2班为(1-10%)x人,
则根据题意得:$\frac{1800}{x}$×+4=$\frac{1800}{(1-10%)x}$,
解得:x=50,
经检验x=50是原方程的根,
则(1-10%)x=45,
答:1班有50人,2班有45人.
点评 本题考查了分式方程的应用,找到合适的等量关系是解决问题的关键,本题主要抓住2班比1班人均捐款多4元,2班的人数比1班的人数少10%等语句进行列式.


科目:初中数学 来源: 题型:解答题
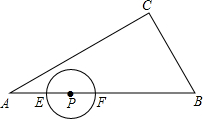 如图,在Rt△ABC中,∠C=90°,BC=3,∠A=30°,点P在AB上,AP=2.点E、F同时从点P出发,分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立刻以原速度沿AB向点B运动,点F运动到点B时停止,点E也运动到点B时停止.在点E、F运动过程中,以EF为直径作圆.设点E运动的时间为t秒.
如图,在Rt△ABC中,∠C=90°,BC=3,∠A=30°,点P在AB上,AP=2.点E、F同时从点P出发,分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立刻以原速度沿AB向点B运动,点F运动到点B时停止,点E也运动到点B时停止.在点E、F运动过程中,以EF为直径作圆.设点E运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2+2ax+4x2 | B. | -a2-4ax+4x2 | C. | -2x+1+4x2 | D. | x4+4+4x2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | $\sqrt{2}•\sqrt{3}=\sqrt{6}$ | C. | a6÷a2=a3 | D. | $\sqrt{(-2}{)^2}=-2$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com