
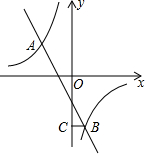
 如图,在平面直角坐标系中,双曲线y=
如图,在平面直角坐标系中,双曲线y=| m |
| x |
| m |
| x |
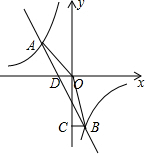 解:(1)∵A(-3,2)在反比例y=
解:(1)∵A(-3,2)在反比例y=| m |
| x |
| 6 |
| x |
| 6 |
| x |
|
|
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2 000名学生的数学成绩进行统计分析,相应数据的统计图表如下:
某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2 000名学生的数学成绩进行统计分析,相应数据的统计图表如下:| 等第 人数 类别 | A | B | C | D |
| 农村 | 200 | 240 | 80 | |
| 县镇 | 290 | 132 | 130 | |
| 城市 | 240 | 132 | 48 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 4 |
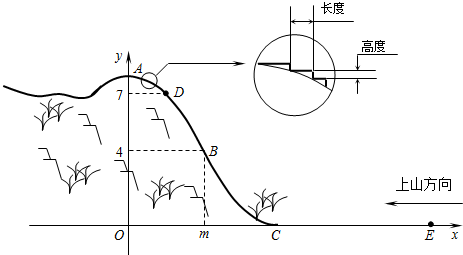
| 1 |
| 28 |
查看答案和解析>>
科目:初中数学 来源: 题型:
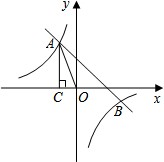 如图,直线y=ax+b与双曲线y=
如图,直线y=ax+b与双曲线y=| k |
| x |
| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
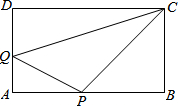 如图:在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从A开始向点B以2厘米/秒的速度移动,点Q沿DA边从D开始向点A以1厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).
如图:在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从A开始向点B以2厘米/秒的速度移动,点Q沿DA边从D开始向点A以1厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com