
【题目】问题发现:
(1)如图1,![]() 内接于半径为4的
内接于半径为4的![]() ,若
,若![]() ,则
,则![]() _______;
_______;
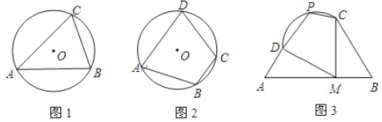
问题探究:
(2)如图2,四边形![]() 内接于半径为6的
内接于半径为6的![]() ,若
,若![]() ,求四边形
,求四边形![]() 的面积最大值;
的面积最大值;
解决问题
(3)如图3,一块空地由三条直路(线段![]() 、AB、
、AB、![]() )和一条弧形道路
)和一条弧形道路![]() 围成,点
围成,点![]() 是
是![]() 道路上的一个地铁站口,已知
道路上的一个地铁站口,已知![]()
![]() 千米,
千米,![]() 千米,
千米,![]() ,
,![]() 的半径为1千米,市政府准备将这块空地规划为一个公园,主入口在点
的半径为1千米,市政府准备将这块空地规划为一个公园,主入口在点![]() 处,另外三个入口分别在点
处,另外三个入口分别在点![]() 、
、![]() 、
、![]() 处,其中点
处,其中点![]() 在
在![]() 上,并在公园中修四条慢跑道,即图中的线段
上,并在公园中修四条慢跑道,即图中的线段![]() 、
、![]() 、
、![]() 、
、![]() ,是否存在一种规划方案,使得四条慢跑道总长度(即四边形
,是否存在一种规划方案,使得四条慢跑道总长度(即四边形![]() 的周长)最大?若存在,求其最大值;若不存在,说明理由.
的周长)最大?若存在,求其最大值;若不存在,说明理由.
【答案】(1)![]() ;(2)四边形ABCD的面积最大值是
;(2)四边形ABCD的面积最大值是![]() ;(3)存在,其最大值为
;(3)存在,其最大值为![]() .
.
【解析】
(1)连接OA、OB,作OH⊥AB于H,利用![]() 求出∠AOH=
求出∠AOH=![]() ∠AOB=
∠AOB=![]() ,根据OA=4,利用余弦公式求出AH,即可得到AB的长;
,根据OA=4,利用余弦公式求出AH,即可得到AB的长;
(2)连接AC,由![]() 得出AC=
得出AC=![]() ,再根据四边形
,再根据四边形![]() 的面积=
的面积= ![]() ,当DH+BM最大时,四边形ABCD的面积最大,得到BD是直径,再将AC、BD的值代入求出四边形面积的最大值即可;
,当DH+BM最大时,四边形ABCD的面积最大,得到BD是直径,再将AC、BD的值代入求出四边形面积的最大值即可;
(3)先证明△ADM≌△BMC,得到△CDM是等边三角形,求得等边三角形的边长CD,再根据完全平方公式的关系得出PD=PC时PD+PC最大,根据CD、∠DPC求出PD,即可得到四边形周长的最大值.
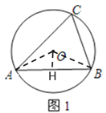
(1)连接OA、OB,作OH⊥AB于H,
∵![]() ,
,
∴∠AOB=120![]() .
.
∵OH⊥AB,
∴∠AOH=![]() ∠AOB=
∠AOB=![]() ,AH=BH=
,AH=BH=![]() AB,
AB,
∵OA=4,
∴AH=![]() ,
,
∴AB=2AH=![]() .
.
故答案为:![]() .
.
(2)∵∠ABC=120![]() ,四边形ABCD内接于
,四边形ABCD内接于![]() ,
,
∴∠ADC=60![]() ,
,
∵![]() 的半径为6,
的半径为6,
∴由(1)得AC=![]() ,
,
如图,连接AC,作DH⊥AC,BM⊥AC,
∴四边形![]() 的面积=
的面积= ![]() ,
,
当DH+BM最大时,四边形ABCD的面积最大,连接BD,则BD是![]() 的直径,
的直径,
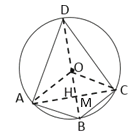
∴BD=2OA=12,BD⊥AC,
∴四边形![]() 的面积=
的面积=![]() .
.
∴四边形ABCD的面积最大值是![]()
(3)存在;
∵![]()
![]() 千米,
千米,![]() 千米,
千米,![]() ,
,
∴△ADM≌△BMC,
∴DM=MC,∠AMD=∠BCM,
∵∠BCM+∠BMC=180![]() -∠B=120
-∠B=120![]() ,
,
∴∠AMD+∠BMC=120![]() ,
,
∴∠DMC=60![]() ,
,
∴△CDM是等边三角形,
∴C、D、M三点共圆,
∵点P在弧CD上,
∴C、D、M、P四点共圆,
∴∠DPC=180![]() -∠DMC=120
-∠DMC=120![]() ,
,
∵![]() 弧的半径为1千米,∠DMC=60
弧的半径为1千米,∠DMC=60![]() ,
,
∴CD=![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴当PD=PC时,PD+PC最大,此时点P在弧CD的中点,交DC于H ,
在Rt△DPH中,∠DHP=90![]() ,∠DPH=60
,∠DPH=60![]() ,DH=
,DH=![]() DC=
DC=![]() ,
,
∴![]() ,
,
∴四边形![]() 的周长最大值=DM+CM+DP+CP=
的周长最大值=DM+CM+DP+CP=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒![]() cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )

A. ![]() B. 2 C. 2
B. 2 C. 2![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形![]() 是矩形,点
是矩形,点![]() ,点
,点![]() ,点
,点![]() .以
.以![]() 点为中心,顺时针旋转矩形
点为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]() ,记旋转角为
,记旋转角为![]() .
.
(1)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
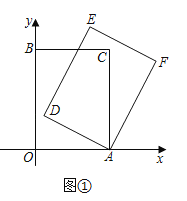
(2)如图②,当点![]() 落在
落在![]() 的延长线上时,求点
的延长线上时,求点![]() 的坐标;
的坐标;

(3)当点![]() 落在线段
落在线段![]() 上时,求点
上时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是⊙
是⊙![]() 的弦,
的弦,![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 的直线交
的直线交![]() 的延长线于点
的延长线于点![]() ,且
,且![]() 是⊙
是⊙![]() 的切线.
的切线.
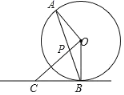
(1)判断![]() 的形状,并说明理由;
的形状,并说明理由;
(2)若![]() ,求
,求![]() 的长;
的长;
(3)设![]() 的面积是
的面积是![]() 的面积是
的面积是![]() ,且
,且![]() .若⊙
.若⊙![]() 的半径为
的半径为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学一幢教学楼的顶部竖有一块写有“校训”的宣传牌![]() ,
,![]() 米,王老师用测倾器在
米,王老师用测倾器在![]() 点测得
点测得![]() 点的仰角为
点的仰角为![]() ,再向教学楼前进9米到达
,再向教学楼前进9米到达![]() 点,测得点
点,测得点![]() 的仰角为
的仰角为![]() ,若测倾器的高度
,若测倾器的高度![]()
![]()
![]() 米,不考虑其它因素,求教学楼
米,不考虑其它因素,求教学楼![]() 的高度.(结果保留根号)
的高度.(结果保留根号)
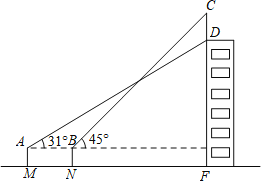
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】富平因取“富庶太平”之意而得名,是华夏文明重要发祥地之一.某班举行关于“美丽的富平”的演讲活动.小明和小丽都想第一个演讲,于是他们通过做游戏来决定谁第一个来演.讲游戏规则是:在一个不透明的袋子中有一个黑球a和两个白球b、c,(除颜色外其它均相同),小丽从袋子中摸出一个球,放回后搅匀,小明再从袋子中摸出一个球,若两次摸到的球颜色相同,则小丽获胜,否则小明获胜,请你用树状图或列表的方法分别求出小丽与小明获胜的概率,并说明这个游戏规则对双方公平吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在BC,CD上,AE=AF,AC与EF相交于点G.下列结论:①AC垂直平分EF;②BE+DF=EF;③当∠DAF=15°时,△AEF为等边三角形;④当∠EAF=60°时,S△ABE=![]() S△CEF.其中正确的是( )
S△CEF.其中正确的是( )
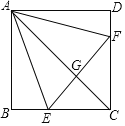
A. ①③B. ②④C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,这个图案是3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.已知AE=5,BE=3,若向正方形ABCD内随意投掷飞镖(每次均落在正方形ABCD内,且落在正方形ABCD内任何一点的机会均等),则恰好落在正方形EFGH内的概率为__________.
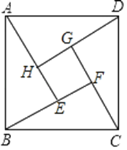
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com