
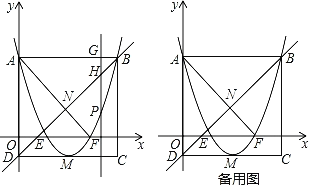
【题目】如图,抛物线y=x2+bx+c经过A (0,3),B (4,3)两点,与x轴交于点E,F,以AB为边作矩形ABCD,其中CD边经过抛物线的项点M,点P是抛物线上一动点(点P不与点A,B重合),过点P作y轴的平行线1与直线AB交于点G,与直线BD交于点H,连接AF交直线BD于点N.
(1)求该抛物线的解析式以及顶点M的坐标;
(2)当线段PH=2GH时,求点P的坐标;
(3)在抛物线上是否存在点P,使得以点P,E,N,F为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=x2﹣4x+3,顶点M的坐标为(2,﹣1);(2)点P的坐标为(﹣1,8)或(3,0);(3)存在点P(2,﹣1)时,使得以点P,E,N,F为顶点的四边形是平行四边形.
【解析】
(1)根据抛物线y=x2+bx+c经过A(0,3),B(4,3)两点,可以求得该抛物线的解析式,然后化为顶点式,即可得到顶点M的坐标;
(2)根据题意,可以表示出线段PH和GH的长,然后即可得到点P的坐标;
(3)根据题意,画出相应的图象,然后利用分类讨论的方法即可得到点P的坐标.
解:(1)∵抛物线y=x2+bx+c经过A(0,3),B(4,3)两点,
∴![]() 得
得![]() ,
,
即该抛物线的解析式为y=x2﹣4x+3,
∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴顶点M的坐标为(2,﹣1);
(2)∵四边形ABCD是矩形,且CD边经过抛物线的顶点M(2,﹣1),
∴D(0,﹣1),
设直线BD的解析式为y=kx+b,
∵直线BD经过点B(4,3),D(0,﹣1),
∴![]() ,
,
解得,![]() ,
,
∴直线BD的解析式为y=x﹣1,
∵点P为是抛物线上一动点,
∴设P(a,a2﹣4a+3),则G(a,3),H(a,a﹣1),
∴PH=|a2﹣4a+3﹣(a﹣1)|=|a2﹣5a+4|,GH=|3﹣(a﹣1)|=|4﹣a|,
∵PH=2GH,
∴|a2﹣5a+4|=2|4﹣a|,
解得,a1=﹣1,a2=3,a3=4,
∴P1(﹣1,8),P2(3,0),P3(4,3),
∵点P不与点A,B重合
∴P3(4,3)不符合要求,
∴当线段PH=2GH时,点P的坐标为P(﹣1,8)或P(3,0);
(3)当y=0时,0=x2﹣4x+3,得x1=3,x2=1,
则点E的坐标为(1,0),点F的坐标为(3,0),
∵A(0,3),F(3,0),
∴直线AF的解析式为y=﹣x+3,
联立![]() ,得
,得![]() ,
,
∴N(2,1),
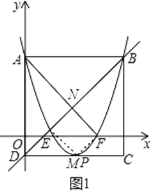
如图1所示,当点P在直线EF下方时,
∵M(2,﹣1),N(2,1),E(1,0),F(3,0),
∴MN与EF互相垂直平分,
∴当点P在点M的位置时,四边形PENF是平行四边形,
此时P(2,﹣1);
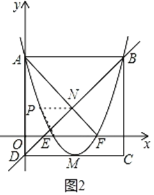
如图2所示,当点P在点E的左侧时,
若四边形PEFN是平行四边形,则P(0,1),
∵抛物线经过点A(0,3),
∴P(0,1)不符合实际,舍去;
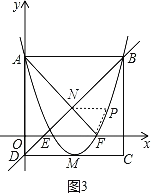
如图3所示,当点P在点F的右侧时,
若四边形PFEN是平行四边形,则P(4,1),
∵抛物线经过点B(4,3),
∴P(4,1)不符合实际,舍去;
综上所述,存在点P(2,﹣1)时,使得以点P,E,N,F为顶点的四边形是平行四边形.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】某文体商店计划购进一批同种型号的篮球和同种型号的排球,每一个排球的进价是每一个篮球的进价的90%,用3600元购买排球的个数要比用3600元购买篮球的个数多10个.
(1)问每一个篮球、排球的进价各是多少元?
(2)该文体商店计划购进篮球和排球共100个,且排球个数不低于篮球个数的3倍,篮球的售价定为每一个100元,排球的售价定为每一个90元.若该批篮球、排球都能卖完,问该文体商店应购进篮球、排球各多少个才能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对折矩形纸片ABCD使AD与BC重合,得到折痕MN,再把纸片展平.E是AD上一点,将△ABE沿BE折叠,使点A的对应点A′落在MN上.若CD=5,则BE的长是_____.
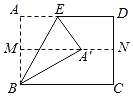
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=-2x+4与x轴交于点A,与y轴交于点B,将△AOB沿直线AB翻折后,设点O的对应点为点C,双曲线y=![]() (x>0)经过点C,则k的值为____________.
(x>0)经过点C,则k的值为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°.
(1)用尺规作∠A的平分线交BC边于点D(不写作法,保留作图痕迹);
(2)在(1)的基础上,已知∠B=30°,AC=6,则线段AD的长是 .
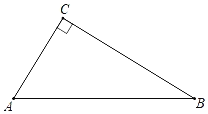
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中秋佳节时,我国有赏月和吃月饼的传统,某校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了60名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图.

(注:参与问卷调查的每一位同学在任何一种分类统计中只有一种选择)
请根据统计图完成下列问题:
(1)扇形统计图中,“很喜欢”的部分所对应的圆心角为__________度;条形统计图中,很喜欢“豆沙”月饼的学生有__________人;
(2)若该校共有学生900人,请根据上述调查结果,估计该校学生中“很喜欢”和“比较喜欢”月饼的共有__________人.
(3)甲同学最爱吃云腿月饼,乙同学最爱吃豆沙月饼,现有重量、包装完全一样的云腿、豆沙、莲蓉、蛋黄四种月饼各一个,让甲、乙每人各选一个,请用画树状图法或列表法,求出甲、乙两人中有且只有一人选中自己最爱吃的月饼的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①、图②均是6×6的正方形网格,每个小正方形的边长为1,小正方形的顶点称为格点,点A、B、C、D均在格点上.用直尺在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写画法.
(1)在图①中以线段AB为腰画一个等腰三角形ABM,画出的△ABM的面积是 .
(2)在图②中以线段CD为边画一个四边形CDEF,使∠FCD+∠EDC=90°.
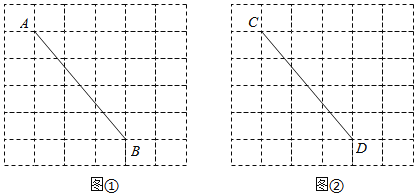
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断中:①abc>0;②b2﹣4ac>0;③9a﹣3b+c=0;④若点(![]() ,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑤5a﹣2b<0;其中正确的个数有( )
,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑤5a﹣2b<0;其中正确的个数有( )
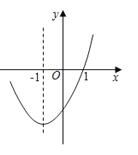
A.2B.3C.4D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com