
| A. |  | B. |  | ||
| C. |  | D. | 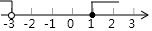 |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知正方形铁丝框ABCD边长为10,现使其变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形的面积为( )
如图,已知正方形铁丝框ABCD边长为10,现使其变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形的面积为( )| A. | 50 | B. | 100 | C. | 150 | D. | 200 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
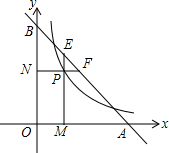 如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数y=$\frac{k}{x}$(x>0)图象上位于直线下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于AB于点F,且AF•BE=8,则k=4.
如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数y=$\frac{k}{x}$(x>0)图象上位于直线下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于AB于点F,且AF•BE=8,则k=4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B的距离,但绳子不够,一位同学帮他想了一个主意:先在地上取一个可以直接达到A的点C,找到AC,BC的中点D,E,并且量得DE的长为15米,则A,B两点间的距离是( )
如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B的距离,但绳子不够,一位同学帮他想了一个主意:先在地上取一个可以直接达到A的点C,找到AC,BC的中点D,E,并且量得DE的长为15米,则A,B两点间的距离是( )| A. | 15米 | B. | 20米 | C. | 30米 | D. | 40米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一次函数y1=x与二次函数y2═ax2+bx+c图象相交于P,Q两点,对于函数y3═ax2+(b-1)x+c,有下列结论:
如图,一次函数y1=x与二次函数y2═ax2+bx+c图象相交于P,Q两点,对于函数y3═ax2+(b-1)x+c,有下列结论:| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com