
 如图,一次函数y1=x与二次函数y2═ax2+bx+c图象相交于P,Q两点,对于函数y3═ax2+(b-1)x+c,有下列结论:
如图,一次函数y1=x与二次函数y2═ax2+bx+c图象相交于P,Q两点,对于函数y3═ax2+(b-1)x+c,有下列结论:| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 ②由抛物线的开口即对称轴即可得出a>0、b<0,②不符合题意;①根据x=1时y>0即可得出a+c>-b,由b<0即可得出a+c>0,①符合题意;③将y1=x代入y2═ax2+bx+c中可得出ax2+(b-1)x+c=0,观察图形可知该方程有两个不相等的正根,由此即可得出函数y3═ax2+(b-1)x+c的图象与x轴的两个交点都在正半轴上,③符合题意.综上即可得出结论.
解答 解:②∵抛物线开口向上,
∴a>0.
∵抛物线的对称轴x=-$\frac{b}{2a}$>0,
∴b<0,②不符合题意;
①∵当x=1时,y=a+b+c>0,
∴a+c>-b>0,①符合题意;
③将y1=x代入y2═ax2+bx+c中,整理得:ax2+(b-1)x+c=0,
观察图形可知,该方程有两个不相等的解,分别为点P、Q的横坐标,
∴函数y3═ax2+(b-1)x+c的图象与x轴的两个交点都在正半轴上,③符合题意.
故选C.
点评 本题考查了二次函数图象与系数的关系以及抛物线与x轴的交点,逐一分析三条结论的正误是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | (-xy)3=-xy3 | B. | (2x2y)2=2x4y2 | C. | ($\frac{2}{3}$x2y)2=$\frac{3}{4}$x4y2 | D. | ($\frac{1}{3}$xy2)3=$\frac{1}{27}$x3y6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | ||
| C. |  | D. | 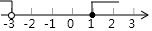 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
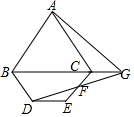 如图,等边三角形ABC中,AB=3,点D是△ABC外一点,连接BD,将线段BD绕点D顺时针旋转120°得到线段DE,连接CE,点F事CE的中点,射线DF与BC边的延长线交于点G,连接AG,若∠CBD=60°,∠ACE=90°,则线段AG的长为$\sqrt{13}$.
如图,等边三角形ABC中,AB=3,点D是△ABC外一点,连接BD,将线段BD绕点D顺时针旋转120°得到线段DE,连接CE,点F事CE的中点,射线DF与BC边的延长线交于点G,连接AG,若∠CBD=60°,∠ACE=90°,则线段AG的长为$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD的对角线BD上取一点E,使得BE=$\frac{1}{4}$BD,延长AE交BC于G,交DC的延长线于F,求:S△CFG:S△BEG的值.
如图,在?ABCD的对角线BD上取一点E,使得BE=$\frac{1}{4}$BD,延长AE交BC于G,交DC的延长线于F,求:S△CFG:S△BEG的值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 1个 | C. | 4个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.927×1010 | B. | 92.7×1010 | C. | 9.27×1011 | D. | 9.27×109 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com