
分析 设相遇时客车行驶了x千米,则小汽车行驶了(x+70)千米,根据路程=客车行驶的路程+小汽车行驶的路程即可得出关于x的一元一次方程,解之即可得出x的值,再根据速度=路程÷时间即可求出小汽车和客车的平均速度.
解答 解:设相遇时客车行驶了x千米,则小汽车行驶了(x+70)千米,
根据题意得:x+x+70=420,
解得:x=175,
∴x+70=245.
175÷2.5=70(千米/小时),
245÷2.5=98(千米/小时).
答:小汽车的平均速度为98千米/小时,客车的平均速度为70千米/小时.
点评 本题考查了一元一次方程的应用,根据路程=客车行驶的路程+小汽车行驶的路程列出关于x的一元一次方程.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
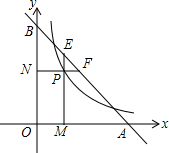 如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数y=$\frac{k}{x}$(x>0)图象上位于直线下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于AB于点F,且AF•BE=8,则k=4.
如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数y=$\frac{k}{x}$(x>0)图象上位于直线下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于AB于点F,且AF•BE=8,则k=4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B的距离,但绳子不够,一位同学帮他想了一个主意:先在地上取一个可以直接达到A的点C,找到AC,BC的中点D,E,并且量得DE的长为15米,则A,B两点间的距离是( )
如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B的距离,但绳子不够,一位同学帮他想了一个主意:先在地上取一个可以直接达到A的点C,找到AC,BC的中点D,E,并且量得DE的长为15米,则A,B两点间的距离是( )| A. | 15米 | B. | 20米 | C. | 30米 | D. | 40米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一次函数y1=x与二次函数y2═ax2+bx+c图象相交于P,Q两点,对于函数y3═ax2+(b-1)x+c,有下列结论:
如图,一次函数y1=x与二次函数y2═ax2+bx+c图象相交于P,Q两点,对于函数y3═ax2+(b-1)x+c,有下列结论:| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
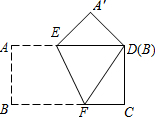 把一张矩形纸片ABCD按如图所示的方式折叠,使顶点B和D重合,折痕为EF.
把一张矩形纸片ABCD按如图所示的方式折叠,使顶点B和D重合,折痕为EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com