
如图,▱ABCD的两条对角线AC和BD相交于点O,并且BD=4,AC=6,BC=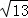 .
.
(1)AC与BD有什么位置关系?为什么?
(2)四边形ABCD是菱形吗?为什么?

科目:初中数学 来源:2013年初中毕业升学考试(新疆区、兵团卷)数学(解析版) 题型:解答题
如图,▱ABCD中,点O是AC与BD的交点,过点O的直线与BA、DC的延
长线分别交于点E、F.
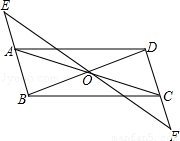
(1)求证:△AOE≌△COF;
(2)请连接EC、AF,则EF与AC满足什么条件时,四边形AECF是矩形,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(福建漳州卷)数学(解析版) 题型:解答题
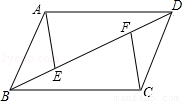
如图,▱ABCD中,E,F是对角线BD上两点,且BE=DF.
(1)图中共有 对全等三角形;
(2)请写出其中一对全等三角形: ≌ ,并加以证明.
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(湖北十堰卷)数学(解析版) 题型:填空题
如图,▱ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=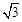 ,则AB的长是
.
,则AB的长是
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com