Question

2．已知抛物线y=ax²-2ax+a-4与x轴分别交于A，B，与y轴交于C点，顶点为P．
（1）直接写出此抛物线的对称轴．
（2）连接BP，Q点是抛物线上一动点（不与P点重合），过Q点的直线y=-3x+b与直线BP相交所成的锐角为45度，求此抛物线的解析式；
（3）平移（2）中的抛物线，使抛物线的顶点在直线CP上滑动，滑动之后的抛物线顶点记为点P'，且与PC交于另一点R．若点M在直线AC上方，且为（2）中的抛物线上点，当以M，P'，R三点为顶点的三角形是含30°角的直角三角形时，求出所有符合条件的M的坐标．

Answer 1

分析 （1）将解析式配成顶点式即可；
（2）只要确定B点坐标就能解决问题．由于平移并不影响两条直线之间的夹角，所以将直线y=-3x+b平移至过P点的位置，设此时的直线y=-3x+b与y轴交于点D，则D点坐标可求，设出B点坐标，过点DE垂直PB于E，在Rt△BOD与Rt△DEB中用勾股定理建立方程，解之即可．
（3）线段CP的长度可求，并且在抛物线滑动过程中，线段P'R的长度也是不变的，始终等于CP，因此，问题就相当于一条定长线段P'R在直线CP上滑动，若M，P'，R三点为顶点的三角形是含30°角的直角三角形，则存在以下三种情况：
①P'R是30°所对的直角边，此时，问题的本质就是M点到P'R的距离为$\sqrt{3}$P'R；
②P'R是60°所以的直角边，此时，问题的本质就是M点到P'R的距离为$\frac{\sqrt{3}}{3}$P'R；
③P'R是斜边，此时，问题的本质就是M点到P'R的距离为$\frac{\sqrt{3}}{4}$P'R；
对于以上三种情况，只需将直线CP平移相应的距离，将平移后的直线解析式与原抛物线解析式联立即可解得M点的坐标．

解答 解：（1）∵y=ax²-2ax+a-4=a（x-1）²-4，
∴抛物线的对称轴为x=1；
（2）平移直线y=-3x+b，使其刚好过P点，
∵P（1，-4），
∴-3+b=-4，
∴b=-1，
∴y=-3x-1，
设直线y=-3x-1与y轴交于点D，连接BD、PB，过点D作DE⊥PB于E，如图1，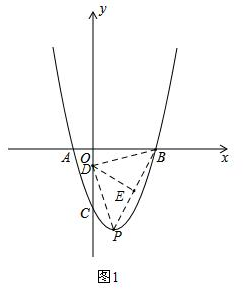

∵P（1，-4），D（0，-1），
∴PD=$\sqrt{10}$，
∵∠DPB=45°，
∴DE=PE=$\sqrt{5}$，
设B（n，0），则PB=$\sqrt{（n-1）^{2}+16}$，
∴BE=PB-PE=$\sqrt{{（n-1）}^{2}+16}-\sqrt{5}$，
∵DE²+BE²=BO²+OD²，
∴$5+（\sqrt{{（n-1）}^{2}+16}-\sqrt{5}）^{2}={n}^{2}+1$，
化简整理得：n²+4n-21=0，
解得：n=3或n=-7（舍去）；
∴B（3，0），
∴0=4a-4，
∴a=1，
∴抛物线的解析式为：y=（x-1）²-4=x²-2x-3；
（3）∵C（0，-3），P（1，-4），
∴CP=$\sqrt{2}$；
抛物线滑动过程中，P'与P为对应点，R与C为对应点，
∴P'R=CP=$\sqrt{2}$；
①若∠P'MR=30°，∠MRP'=90°（也可以是∠MP'R=90°，没有任何影响），如图2，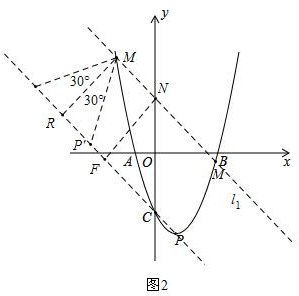

此时，MR=$\sqrt{3}P'R=\sqrt{6}$，
设过点M且平行于直线CP的直线为l₁，l₁与y轴的交点为N，过点N作NF⊥CP于F，则NF=MR=$\sqrt{6}$，
∵C（0，-3），P（1，-4），
∴直线CP的解析式为：y=-x-3，
∴∠FCN=45°，
即△NFC是等腰直角三角形，
∴CN=$\sqrt{2}NF$=2$\sqrt{3}$，
∴l₁相当于CP向上平移2$\sqrt{3}$个单位得到，
∴l₁的解析式为：y=-x+2$\sqrt{3}$-3，
联立方程组：$\left\{\begin{array}{l}{y=-x+2\sqrt{3}-3}\\{y={x}^{2}-2x-3}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{{x}_{1}=\frac{1-\sqrt{1+8\sqrt{3}}}{2}}\\{{y}_{1}=\frac{\sqrt{1+8\sqrt{3}}+4\sqrt{3}-7}{2}}\end{array}\right.$，$\left\{\begin{array}{l}{{x}_{2}=\frac{1+\sqrt{1+8\sqrt{3}}}{2}}\\{{y}_{2}=\frac{4\sqrt{3}-\sqrt{1+8\sqrt{3}}-7}{2}}\end{array}\right.$，
∴M点的坐标为：（$\frac{1-\sqrt{1+8\sqrt{3}}}{2}$，$\frac{\sqrt{1+8\sqrt{3}+4\sqrt{3}}-7}{2}$），（$\frac{1+8\sqrt{3}}{2}$，$\frac{4\sqrt{3}-\sqrt{1+8\sqrt{3}}-7}{2}$）；

②若∠MRP'=30°，∠MP'R=90°，如图3，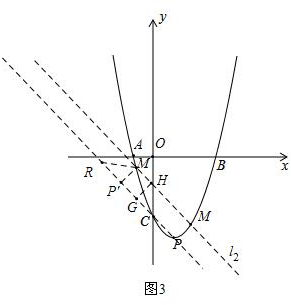

此时，MP'=$\frac{\sqrt{3}}{3}P'R=\frac{\sqrt{6}}{3}$，
设过点M且平行于直线CP的直线为l₂，l₂与y轴的交点为H，过点H作HG⊥CP于G，则HG=MP'=$\frac{\sqrt{6}}{3}$，
∴CH=$\frac{2\sqrt{3}}{3}$，
∴l₂相当于CP向上平移$\frac{2\sqrt{3}}{3}$个单位得到，
∴l₂的解析式为：y=-x+$\frac{2\sqrt{3}}{3}$-3，
联立方程组$\left\{\begin{array}{l}{y=-x+\frac{2\sqrt{3}}{3}-3}\\{y={x}^{2}-2x-3}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{{x}_{3}=\frac{3-\sqrt{9+24\sqrt{3}}}{6}}\\{{y}_{3}=\frac{\sqrt{9+24\sqrt{3}}+4\sqrt{3}-21}{6}}\end{array}\right.$（舍去），$\left\{\begin{array}{l}{{x}_{4}=\frac{3+\sqrt{9+24\sqrt{3}}}{6}}\\{{y}_{4}=\frac{\sqrt{9+24\sqrt{3}}+4\sqrt{3}-15}{6}}\end{array}\right.$；
∴M点的坐标为：（$\frac{3+\sqrt{9+24\sqrt{3}}}{6}$，$\frac{\sqrt{9+24\sqrt{3}}+4\sqrt{3}-15}{6}$）；
③若P'R为斜边，如图4所示，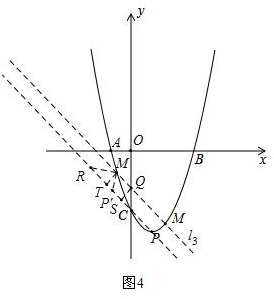

作MT⊥RP'于T，则MT=$\frac{\sqrt{3}}{2}P'R$=$\frac{\sqrt{6}}{4}$，
设过点M且平行于PC的直线为l₃，l₃与y轴的交点为Q，过点Q作QS⊥PC于点S，则QS=MT=$\frac{\sqrt{6}}{4}$，
∴CQ=$\frac{\sqrt{3}}{2}$，
∴l₃相当于直线CP向上平移$\frac{\sqrt{3}}{2}$个单位得到的，
∴l₃的解析式为：y=-x+$\frac{\sqrt{3}}{2}$-3，
联立方程组：$\left\{\begin{array}{l}{y=-x+\frac{\sqrt{3}}{2}-3}\\{y={x}^{2}-2x-3}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{{x}_{5}=\frac{1-\sqrt{1+2\sqrt{3}}}{2}}\\{{y}_{5}=\frac{\sqrt{1+2\sqrt{3}}+\sqrt{3}-7}{2}}\end{array}\right.$（舍去），$\left\{\begin{array}{l}{{x}_{6}=\frac{1+\sqrt{1+2\sqrt{3}}}{2}}\\{{y}_{6}=\frac{\sqrt{3}-\sqrt{1+2\sqrt{3}}-7}{2}}\end{array}\right.$；

∴M点的坐标为：（$\frac{1+\sqrt{1+2\sqrt{3}}}{2}$，$\frac{\sqrt{3}-\sqrt{1+2\sqrt{3}}-7}{2}$）；
综上所述，满足要求的M点坐标为：（$\frac{1-\sqrt{1+8\sqrt{3}}}{2}$，$\frac{\sqrt{1+8\sqrt{3}+4\sqrt{3}}-7}{2}$），（$\frac{1+8\sqrt{3}}{2}$，$\frac{4\sqrt{3}-\sqrt{1+8\sqrt{3}}-7}{2}$），
（$\frac{3+\sqrt{9+24\sqrt{3}}}{6}$，$\frac{\sqrt{9+24\sqrt{3}}+4\sqrt{3}-15}{6}$），（$\frac{1+\sqrt{1+2\sqrt{3}}}{2}$，$\frac{\sqrt{3}-\sqrt{1+2\sqrt{3}}-7}{2}$）；

点评 本题考查了二次函数的顶点式、解直角三角形、勾股定理、待定系数法求抛物线解析式、特殊角的三角函数、两点间的距离公式、直线的平移、抛物线的滑动，解二元二次方程组等众多的知识点，难度很大，是一道经典压轴题．本题仅第（2）问求解析式就有一定难度，需要一定理几何技巧．第（3）问是抛物线滑动问题，类似于2013成都中考28题第（2）问第一小问，同学们可以对比进行研究．