【题目】已知 A，B，C 三点都在直线l 上，AC 与 BC 的长度之比为 2：3，D 是 AB 的中点．若 AC4cm，则 CD 的长为 ________________ cm．
【答案】1cm或5cm
【解析】
由于点A、B、C三点都在直线l 上，故分点C在AB之间与点C在AB外两种情况进行讨论．当C在AB之间时，AB=AC+BC，；当C在AB外时，此时AB=BC-AC，再根据D 是 AB 的中点，先求出AD，即可求出CD的长．
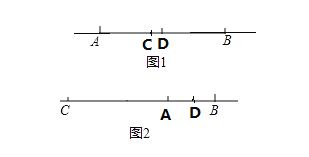
如图1所示，
∵线段AC4cm，AC 与 BC 的长度之比为 2：3，
∴BC=6cm，
∴AB=AC+BC=4cm +6cm=10cm，
∵D 是 AB 的中点，
∴AD=
AB=5cm，
∴CD=AD-AC=5cm-4cm=1cm；
如图2所示，
∵线段AC4cm，AC 与 BC 的长度之比为 2：3，
∴BC=6cm，
∴AB=BC-AC=6cm -4cm=2cm，
∵D 是 AB 的中点，
∴AD=AB=1cm，
∴CD=AD+AC=1cm+4cm=5cm.
故答案为：1cm或5cm.
科目：初中数学 来源： 题型：
【题目】某水果种植场今年收获的“妃子笑”和“无核Ⅰ号”两种荔枝共3200 千克，全部售出后卖了30400 元．已知“妃子笑”荔枝每千克售价8 元，“无核Ⅰ号”荔枝每千克售价12 元，问该种植场今年这两种荔枝各收获多少千克？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，O为直线AB上一点，∠AOC＝50°，OD平分∠AOC，∠DOE＝90°，
(1)求∠BOC的度数；
(2)通过计算判断OE是否平分∠BOC.
查看答案和解析>>
科目：初中数学 来源： 题型：
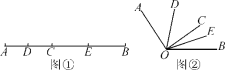
【题目】如图①，已知线段AB＝16 cm，点C为线段AB上的一个动点(点C不与A，B重合)，点D，E分别是AC和BC的中点．
(1)求DE的长；
(2)知识迁移：如图②，已知∠AOB＝130°，过角的内部任一点C画射线OC，若OD，OE分别平分∠AOC和∠BOC，试说明∠DOE的大小与射线OC的位置无关．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】随着地铁和共享单车的发展，“地铁+单车”已成为很多市民出行的选择，李华从文化宫站出发，先乘坐地铁，准备在离家较近的A，B，C，D，E中的某一站出地铁，再骑共享单车回家，设他出地铁的站点与文化宫距离为x（单位：千米），乘坐地铁的时间y1（单位：分钟）是关于x的一次函数，其关系如下表：
地铁站 | A | B | C | D | E |
x（千米） | 8 | 9 | 10 | 11.5 | 13 |
y1（分钟） | 18 | 20 | 22 | 25 | 28 |
（1）求y1关于x的函数表达式；
（2）李华骑单车的时间（单位：分钟）也受x的影响，其关系可以用y2= 
x2﹣11x+78来描述，请问：李华应选择在那一站出地铁，才能使他从文化宫回到家所需的时间最短？并求出最短时间．
查看答案和解析>>
科目：初中数学 来源： 题型：
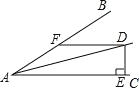
【题目】如图∠BAC=30°，D 为角平分线上一点，DE⊥AC 于 E，DF∥AC且交AB于F．
（1）求证：△ADF 是等腰三角形．
（2）若 DF=10cm，求 DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平面直角坐标系中，已知点A（-3，3），B（-5，1），C（-2，0），P（a，b）是△ABC的边AC上任意一点，△ABC经过平移后得到△A1B1C1，点P的对应点为P1（a+6，b-2）．
（1）直接写出点C1的坐标；
（2）在图中画出△A1B1C1；
（3）求△AOA1的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
