
【题目】
(1)计算:| ![]() ﹣1|﹣
﹣1|﹣ ![]() +2sin45°+(
+2sin45°+( ![]() )﹣2;
)﹣2;
(2)解不等式组:  .
.
【答案】
(1)解:原式= ![]() ﹣1﹣2
﹣1﹣2 ![]() +2×
+2× ![]() +4
+4
= ![]() ﹣1﹣2
﹣1﹣2 ![]() +
+ ![]() +4
+4
=3
(2)解: 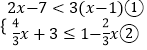 ,
,
①可化简为2x﹣7<3x﹣3,
﹣x<4,
x>﹣4,
②可化简为2x≤1﹣3,则x≤﹣1.
不等式的解集是﹣4<x≤﹣1
【解析】(1)原式利用二次根式性质,特殊角的三角函数值,以及负整数指数幂法则计算即可得到结果.(2)分别求得两个不等式的解集,然后取其公共部分即可.
【考点精析】解答此题的关键在于理解整数指数幂的运算性质的相关知识,掌握aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数),以及对一元一次不等式组的解法的理解,了解解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).


科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )
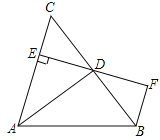
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 A,B,C 三点都在直线l 上,AC 与 BC 的长度之比为 2:3,D 是 AB 的中点.若 AC4cm,则 CD 的长为 ________________ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,抛物线C:y=ax2+bx+c与x轴相交于A,B两点,顶点为D(0,4),AB=4 ![]() ,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C′.
,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C′.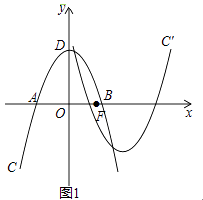
(1)求抛物线C的函数表达式;
(2)若抛物线C′与抛物线C在y轴的右侧有两个不同的公共点,求m的取值范围.
(3)如图2,P是第一象限内抛物线C上一点,它到两坐标轴的距离相等,点P在抛物线C′上的对应点P′,设M是C上的动点,N是C′上的动点,试探究四边形PMP′N能否成为正方形?若能,求出m的值;若不能,请说明理由.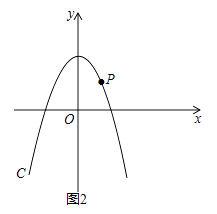
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全球气候变暖导致-些冰川融化并消失,在冰川|消失12年后,一种低等植物苔藓,就开始在岩石上生长,每一个苔藓都会长成近似的圆形,苔藓的直径和其生长年限近似地满足如下的关系式:d=7![]() (t≥12),其中d表示苔藓的直径,单位是厘米,t代表冰川消失的时间(单位:年)。
(t≥12),其中d表示苔藓的直径,单位是厘米,t代表冰川消失的时间(单位:年)。
(1)计算冰川消失16年后苔藓的直径为多少厘米?
(2)如果测得一些苔藓的直径是35厘米,问冰川约是在多少年前消失的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在5×5的正方形网格中,每个小正方形的边长均为1,线段AB的端点在格点上,按要求画出格点三角形,并求其面积.
(1)在图①中画出一个以 AB为腰的等腰三角形 ABC,其面积为____________.
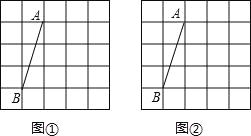
(2) 在图②中画出一个以AB为底的等腰三角形ABC,其面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,直接写出它的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE.
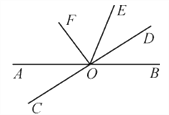
(1)判断OF与OD的位置关系;
(2)若∠AOC∶∠AOD=1∶5,求∠EOF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com