练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在5×5的正方形网格中，每个小正方形的边长均为1，线段AB的端点在格点上，按要求画出格点三角形，并求其面积．

    （1）在图①中画出一个以 AB为腰的等腰三角形 ABC，其面积为____________.

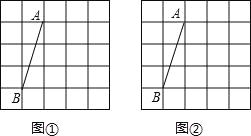
    （2） 在图②中画出一个以AB为底的等腰三角形ABC，其面积为__________.

    【答案】（1）图见解析；面积为：4或5或3；（2）图见解析；面积为：2.5．

    【解析】

    （1）根据所画的等腰三角形,数格点或用割补法分别求出边长和高线长,即可求出面积,

    （2）运用割补法,求出三角形ABC所在矩形的面积,减去多余的三个三角形面积即可.

    解：（1）以 AB 为腰的等腰三角形的面积：×2×3=3；

    面积为：4或5或3；

    （2）以 AB 为底的等腰三角形的面积：2×3﹣×3×1﹣×1×2×2=2.5，

    故答案为3，2.5．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为积极响应南充市创建“全国卫生城市”的号召，某校1 500名学生参加了卫生知识竞赛，成绩记为A、B、C、D四等。从中随机抽取了部分学生成绩进行统计，绘制成如下两幅不完整的统计图表，根据图表信息，以下说法不正确的是（ ）

    A．样本容量是200

    B．D等所在扇形的圆心角为15°

    C．样本中C等所占百分比是10%

    D．估计全校学生成绩为A等大约有900人

    查看答案和解析>>

    科目：初中数学 来源： 题型：

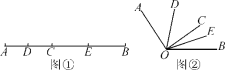
    【题目】如图①，已知线段AB＝16 cm，点C为线段AB上的一个动点(点C不与A，B重合)，点D，E分别是AC和BC的中点．

    (1)求DE的长；

    (2)知识迁移：如图②，已知∠AOB＝130°，过角的内部任一点C画射线OC，若OD，OE分别平分∠AOC和∠BOC，试说明∠DOE的大小与射线OC的位置无关．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】
    （1）计算：| ﹣1|﹣ +2sin45°+（ ）﹣2；
    （2）解不等式组： ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

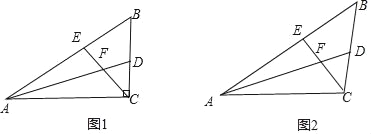
    【题目】如图1，在△ABC中，∠ACB是直角，∠B＝60°，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F．

    (1)直接写出∠AFC的度数：　 　；

    (2)请你判断并写出FE与FD之间的数量关系；

    (3)如图2，在△ABC中，如果∠ACB不是直角，而(1)中的其它条件不变，试判断线段AE、CD与AC之间的数量关系并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

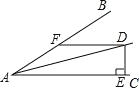
    【题目】如图∠BAC=30°，D 为角平分线上一点，DE⊥AC 于 E，DF∥AC且交AB于F．

    （1）求证：△ADF 是等腰三角形．

    （2）若 DF=10cm，求 DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，A、D、F、B在同一直线上，AD＝BF，AE＝BC，且AE∥BC．

    求证：（1）EF＝CD；（2）EF∥CD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

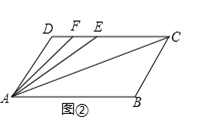
    【题目】如图①，已知AD∥BC，∠B=∠D=120°．

    （1）请问：AB与CD平行吗？为什么？

    （2）若点E、F在线段CD上，且满足AC平分∠BAE，AF平分∠DAE，如图②，求∠FAC的度数．

    （3）若点E在直线CD上，且满足∠EAC=∠BAC，求∠ACD：∠AED的值（请自己画出正确图形，并解答）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

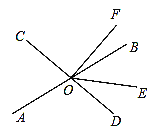
    【题目】直线AB、CD相交于点O，OE平分∠BOD．OF⊥CD，垂足为O，若∠EOF＝54°．

    （1）求∠AOC的度数；

    （2）作射线OG⊥OE，试求出∠AOG的度数．

    查看答案和解析>>

    同步练习册答案