
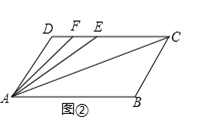
【题目】如图①,已知AD∥BC,∠B=∠D=120°.
(1)请问:AB与CD平行吗?为什么?
(2)若点E、F在线段CD上,且满足AC平分∠BAE,AF平分∠DAE,如图②,求∠FAC的度数.
(3)若点E在直线CD上,且满足∠EAC=![]() ∠BAC,求∠ACD:∠AED的值(请自己画出正确图形,并解答).
∠BAC,求∠ACD:∠AED的值(请自己画出正确图形,并解答).

【答案】(1)平行,理由见解析;(2)∠FAC =30°;(3)∠ACD:∠AED=2:3或2:1.
【解析】试题分析:(1)依据平行线的性质以及判定,即可得到AB∥CD;
(2)依据AC平分∠BAE,AF平分∠DAE,即可得到∠EAC=![]() ∠BAE,∠EAF=
∠BAE,∠EAF=![]() ∠DAE,进而得出∠FAC=∠EAC+∠EAF=
∠DAE,进而得出∠FAC=∠EAC+∠EAF=![]() (∠BAE+∠DAE)=
(∠BAE+∠DAE)=![]() ∠DAB;
∠DAB;
(3)分两种情况讨论:当点E在线段CD上时;当点E在DC的延长线上时,分别依据AB∥CD,进而得到∠ACD:∠AED的值.
试题解析:解:(1)平行.
如图①.∵AD∥BC,∴∠A+∠B=180°.
又∵∠B=∠D=120°,∴∠D+∠A=180°,∴AB∥CD;

(2)如图②.∵AD∥BC,∠B=∠D=120°,∴∠DAB=60°.
∵AC平分∠BAE,AF平分∠DAE,∴∠EAC=![]() ∠BAE,∠EAF=
∠BAE,∠EAF=![]() ∠DAE,
∠DAE,
∴∠FAC=∠EAC+∠EAF=![]() (∠BAE+∠DAE)=
(∠BAE+∠DAE)=![]() ∠DAB=30°;
∠DAB=30°;

(3)①如图3,当点E在线段CD上时,
由(1)可得AB∥CD,∴∠ACD=∠BAC,∠AED=∠BAE.

又∵∠EAC=![]() ∠BAC,∴∠ACD:∠AED=2:3;
∠BAC,∴∠ACD:∠AED=2:3;
②如图4,当点E在DC的延长线上时,
由(1)可得AB∥CD,∴∠ACD=∠BAC,∠AED=∠BAE.
又∵∠EAC=![]() ∠BAC,∴∠ACD:∠AED=2:1.
∠BAC,∴∠ACD:∠AED=2:1.
综上所述:∠ACD:∠AED=2:3或2:1.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在5×5的正方形网格中,每个小正方形的边长均为1,线段AB的端点在格点上,按要求画出格点三角形,并求其面积.
(1)在图①中画出一个以 AB为腰的等腰三角形 ABC,其面积为____________.
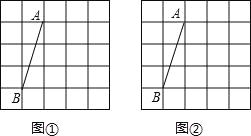
(2) 在图②中画出一个以AB为底的等腰三角形ABC,其面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,直接写出它的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() 的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.
的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA. 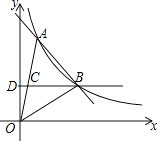
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为6cm,点E、M分别是线段BD、AD上的动点,连接AE并延长,交边BC于F,过M作MN⊥AF,垂足为H,交边AB于点N.
(1)如图1,若点M与点D重合,求证:AF=MN;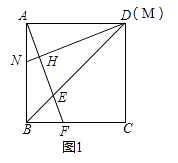
(2)如图2,若点M从点D出发,以1cm/s的速度沿DA向点A运动,同时点E从点B出发,以 ![]() cm/s的速度沿BD向点D运动,运动时间为t s.
cm/s的速度沿BD向点D运动,运动时间为t s.
①设BF=y cm,求y关于t的函数表达式;
②当BN=2AN时,连接FN,求FN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE.
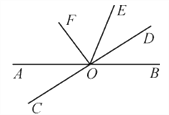
(1)判断OF与OD的位置关系;
(2)若∠AOC∶∠AOD=1∶5,求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
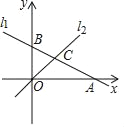
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com