
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() 的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.
的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA. 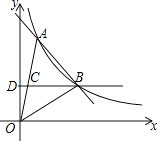
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积.
【答案】
(1)解:如图,过点A作AF⊥x轴交BD于E,
∵点B(3,2)在反比例函数y= ![]() 的图象上,
的图象上,
∴a=3×2=6,
∴反比例函数的表达式为y= ![]() ,
,
∵B(3,2),
∴EF=2,
∵BD⊥y轴,OC=CA,
∴AE=EF= ![]() AF,
AF,
∴AF=4,
∴点A的纵坐标为4,
∵点A在反比例函数y= ![]() 图象上,
图象上,
∴A( ![]() ,4),
,4),
∴ 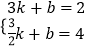 ,
,
∴ 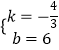 ,
,
∴一次函数的表达式为y=﹣ ![]() x+6
x+6

(2)解:如图1,过点A作AF⊥x轴于F交OB于G,
∵B(3,2),
∴直线OB的解析式为y= ![]() x,
x,
∴G(2, ![]() ),
),
∵A(3,4),
∴AG=4﹣ ![]() =
= ![]() ,
,
∴S△AOB=S△AOG+S△ABG= ![]() ×
× ![]() ×3=4.
×3=4.
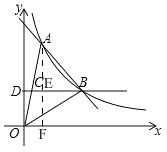
【解析】(1)先利用待定系数法求出反比例函数解析式,进而确定出点A的坐标,再用待定系数法求出一次函数解析式;(2)先求出OB的解析式式,进而求出AG,用三角形的面积公式即可得出结论.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°,
(1)求∠BOC的度数;
(2)通过计算判断OE是否平分∠BOC.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图∠BAC=30°,D 为角平分线上一点,DE⊥AC 于 E,DF∥AC且交AB于F.
(1)求证:△ADF 是等腰三角形.
(2)若 DF=10cm,求 DE的长.
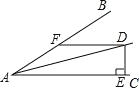
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区①号楼与号楼隔河相望,李明家住在①号楼,他很想知道号楼的高度,于是他做了一些测量,他先在B点测得C点的仰角为60°,然后到42米高的楼顶A处,测得C点的仰角为30°,请你帮助李明计算号楼的高度CD. 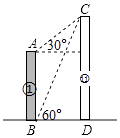
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知AD∥BC,∠B=∠D=120°.
(1)请问:AB与CD平行吗?为什么?
(2)若点E、F在线段CD上,且满足AC平分∠BAE,AF平分∠DAE,如图②,求∠FAC的度数.
(3)若点E在直线CD上,且满足∠EAC=![]() ∠BAC,求∠ACD:∠AED的值(请自己画出正确图形,并解答).
∠BAC,求∠ACD:∠AED的值(请自己画出正确图形,并解答).

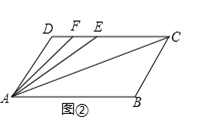
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】双峰县教育局要求各学校加强对学生的安全教育,全县各中小学校引起高度重视,小刚就本班同学对安全知识的了解程度进行了一次调查统计.他将统计结果分为三类,A:熟悉;B:了解较多;C:一般了解。图①和图②是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)求小刚所在的班级共有多少名学生;
(2)在条形图中,将表示“一般了解”的部分补充完整‘’
(3)在扇形统计图中,计算“了解较多”部分所对应的扇形圆心角的度数;
(4)如果小刚所在年级共1000名同学,请你估算全年级对安全知识“了解较多”的学生人数.
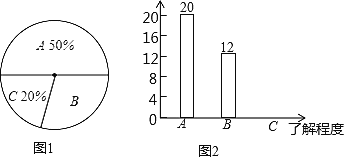
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2).

(1)直接写出点C1的坐标;
(2)在图中画出△A1B1C1;
(3)求△AOA1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
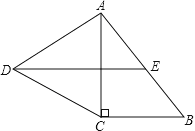
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示.
(1)若区域Ⅰ的三种瓷砖均价为300元/m2 , 面积为S(m2),区域Ⅱ的瓷砖均价为200元/m2 , 且两区域的瓷砖总价为不超过12000元,求S的最大值;
(2)若区域Ⅰ满足AB:BC=2:3,区域Ⅱ四周宽度相等
①求AB,BC的长;
②若甲、丙两瓷砖单价之和为300元/m2 , 乙、丙瓷砖单价之比为5:3,且区域Ⅰ的三种瓷砖总价为4800元,求丙瓷砖单价的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com