
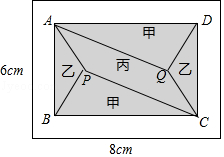
【题目】小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示.
(1)若区域Ⅰ的三种瓷砖均价为300元/m2 , 面积为S(m2),区域Ⅱ的瓷砖均价为200元/m2 , 且两区域的瓷砖总价为不超过12000元,求S的最大值;
(2)若区域Ⅰ满足AB:BC=2:3,区域Ⅱ四周宽度相等
①求AB,BC的长;
②若甲、丙两瓷砖单价之和为300元/m2 , 乙、丙瓷砖单价之比为5:3,且区域Ⅰ的三种瓷砖总价为4800元,求丙瓷砖单价的取值范围.
【答案】
(1)
解:由题意300S+(48﹣S)200≤12000,
解得S≤24.
∴S的最大值为24.
(2)
解:①设区域Ⅱ四周宽度为a,则由题意(6﹣2a):(8﹣2a)=2:3,解得a=1,
∴AB=6﹣2a=4,CB=8﹣2a=6.
②设乙、丙瓷砖单价分别为5x元/m2和3x元/m2,则甲的单价为(300﹣3x)元/m2,
∵PQ∥AD,
∴甲的面积=矩形ABCD的面积的一半=12,设乙的面积为s,则丙的面积为(12﹣s),
由题意12(300﹣3x)+5xs+3x(12﹣s)=4800,
解得s= ![]() ,
,
∵0<s<12,
∴0< ![]() <12,
<12,
∴0<x<50,
∴丙瓷砖单价3x的范围为0<3x<150元/m2.
【解析】(1)根据题意可得300S+(48﹣S)200≤12000,解不等式即可;(2)①设区域Ⅱ四周宽度为a,则由题意(6﹣2a):(8﹣2a)=2:3,解得a=1,由此即可解决问题;②设乙、丙瓷砖单价分别为5x元/m2和3x元/m2 , 则甲的单价为(300﹣3x)元/m2 , 由PQ∥AD,可得甲的面积=矩形ABCD的面积的一半=12,设乙的面积为s,则丙的面积为(12﹣s),由题意12(300﹣3x)+5xs+3x(12﹣s)=4800,解得s= ![]() ,由0<s<12,可得0<
,由0<s<12,可得0< ![]() <12,解不等式即可;
<12,解不等式即可;
【考点精析】认真审题,首先需要了解矩形的性质(矩形的四个角都是直角,矩形的对角线相等).


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() 的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.
的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA. 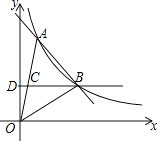
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
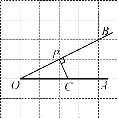
【题目】如图,点P是∠AOB的边OB上的一点,过点P画OB的垂线,交OA于点C.
(1)过点P画OA的垂线,垂足为H;
(2)线段PH的长度是点P到____的距离,____是点C到直线OB的距离.线段PC,PH,OC这三条线段大小关系是___.(用“<”号连接)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,DE是AC的垂直平分线.
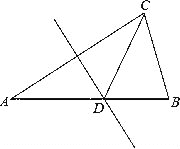
(1)求证:△BCD是等腰三角形;
(2)△BCD的周长是a,BC=b,求△ACD的周长(用含a,b的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
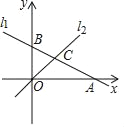
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知□ABCD,AB//x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是□ABCD边上的一个动点.

(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.
(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解江城中学学生的身高情况,随机对该校男生、女生的身高进行抽样调查,已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成如下所示的统计表和如图所示的统计图.
组别 | 身高(cm) |
A | x<150 |
B | 150≤x<155 |
C | 155≤x<160 |
D | 160≤x<165 |
E | x≥165 |
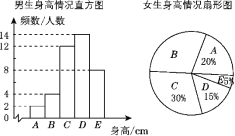
根据图表中提供的信息,回答下列问题:
(1)女生身高在B组的有________人;
(2)在样本中,身高在150≤x<155之间的共有________人,身高人数最多的在________组(填组别序号);
(3)已知该校共有男生500人,女生480人,请估计身高在155≤x<165之间的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点A,B,C在一次函数y=-2x+m的图象上,它们的横坐标依次为-1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )

A. 3(m-1) B. ![]() (m-2) C. 1 D. 3
(m-2) C. 1 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
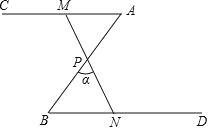
【题目】如图,∠A=∠B=50°,P 为 AB 中点,点 M 为射线 AC 上(不与点 A 重合)的任意点,连接 MP,并使 MP 的延长线交射线 BD 于点 N,设∠ BPN=α.
(1)求证:△APM≌△BPN;
(2)当 MN=2BN 时,求α的度数;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com