
【题目】如图,在△ABC中,AB=AC,∠A=36°,DE是AC的垂直平分线.
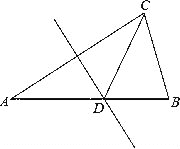
(1)求证:△BCD是等腰三角形;
(2)△BCD的周长是a,BC=b,求△ACD的周长(用含a,b的代数式表示)
【答案】(1)见解析;(2)a﹣b+b+b=a+b.
【解析】试题分析:(1)先由AB=AC,∠A=36°,可求∠B=∠ACB=![]() =72°,然后由DE是AC的垂直平分线,可得AD=DC,进而可得∠ACD=∠A=36°,然后根据外角的性质可求:∠CDB=∠ACD+∠A=72°,根据等角对等边可得:CD=CB,进而可证△BCD是等腰三角形;
=72°,然后由DE是AC的垂直平分线,可得AD=DC,进而可得∠ACD=∠A=36°,然后根据外角的性质可求:∠CDB=∠ACD+∠A=72°,根据等角对等边可得:CD=CB,进而可证△BCD是等腰三角形;
(2)由(1)知:AD=CD=CB=b,由△BCD的周长是a,可得AB=a﹣b,由AB=AC,可得AC=a﹣b,进而得到△ACD的周长=AC+AD+CD=a﹣b+b+b=a+b.
(1)证明:∵AB=AC,∠A=36°,
∴∠B=∠ACB=![]() =72°,
=72°,
∵DE是AC的垂直平分线,
∴AD=DC,
∴∠ACD=∠A=36°,
∵∠CDB是△ADC的外角,
∴∠CDB=∠ACD+∠A=72°,
∴∠B=∠CDB,
∴CB=CD,
∴△BCD是等腰三角形;
(2)解:∵AD=CD=CB=b,△BCD的周长是a,
∴AB=a﹣b,
∵AB=AC,
∴AC=a﹣b,
∴△ACD的周长=AC+AD+CD=a﹣b+b+b=a+b.
点睛:此题考查了等腰三角形的性质,线段垂直平分线的性质以及三角形内角和定理等知.此题综合性较强,但难度不大,解题的关键是注意数形结合思想的应用,注意等腰三角形的性质与等量代换.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,某小区①号楼与号楼隔河相望,李明家住在①号楼,他很想知道号楼的高度,于是他做了一些测量,他先在B点测得C点的仰角为60°,然后到42米高的楼顶A处,测得C点的仰角为30°,请你帮助李明计算号楼的高度CD. 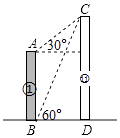
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
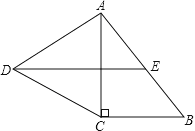
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪得行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为m.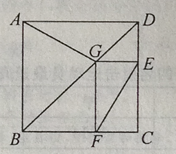
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.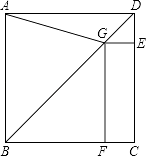
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示.
(1)若区域Ⅰ的三种瓷砖均价为300元/m2 , 面积为S(m2),区域Ⅱ的瓷砖均价为200元/m2 , 且两区域的瓷砖总价为不超过12000元,求S的最大值;
(2)若区域Ⅰ满足AB:BC=2:3,区域Ⅱ四周宽度相等
①求AB,BC的长;
②若甲、丙两瓷砖单价之和为300元/m2 , 乙、丙瓷砖单价之比为5:3,且区域Ⅰ的三种瓷砖总价为4800元,求丙瓷砖单价的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场元旦期间举行优惠活动,对甲、乙两种商品实行打折出售,打折前,购买5间甲商品和1件乙商品需要84元,购买6件甲商品和3件乙商品需要108元,元旦优惠打折期间,购买50件甲商品和50件乙商品仅需960元,这比不打折前节省多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
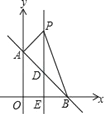
【题目】如图,平面直角坐标系中,直线AB:y=﹣x+b交y轴于点A(0,4),交x轴于点B.
(1)求直线AB的表达式和点B的坐标;
(2)直线l垂直平分OB交AB于点D,交x轴于点E,点P是直线l上一动点,且在点D的上方,设点P的纵坐标为n.
①用含n的代数式表示△ABP的面积;
②当S△ABP=8时,求点P的坐标;
③在②的条件下,以PB为斜边在第一象限作等腰直角△PBC,求点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com