
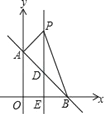
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�ֱ��AB��y=��x+b��y���ڵ�A��0��4������x���ڵ�B��
��1����ֱ��AB�ı���ʽ�͵�B�����ꣻ
��2��ֱ��l��ֱƽ��OB��AB�ڵ�D����x���ڵ�E����P��ֱ��l��һ���㣬���ڵ�D���Ϸ������P��������Ϊn��
���ú�n�Ĵ���ʽ��ʾ��ABP�������
�ڵ�S��ABP=8ʱ�����P�����ꣻ
���ڢڵ������£���PBΪб���ڵ�һ����������ֱ����PBC�����C�����꣮
���𰸡���1��AB:y=-x+4��B(4��0)����2����S��ABP=2n-4����P(2��6)����C(6��4).
�����������������
��1���ѵ�A��0��4������y=��x+b���b��ֵ�����ɵõ�һ�κ����Ľ���ʽ���ɽ���ʽ������õ�B�����ꣻ
��2��������1���������B������Ϊ��4��0����������֪��ֱ��PEΪ�� ![]() ���ɴ˿���õ�D�����꣬�Ӷ����ú���n���Ĵ���ʽ�����PD�ij�����S��ABP=
���ɴ˿���õ�D�����꣬�Ӷ����ú���n���Ĵ���ʽ�����PD�ij�����S��ABP=![]() PD��OB�����ú���n������������
PD��OB�����ú���n������������
����S��ABP=8������������ı���ʽ�����ⷽ�̼��������n����ֵ���Ӷ��ɵô�ʱ��P�����ꣻ
������ͼ�����C1��C2�Ƿ�������ĵ�C�����������ã��ı���BC1PC2�������Σ�����C1��C1M��x���ڵ�M������P��PN����MC1�ڵ�N�����ı���PEMN�Ǿ��Σ���C1MB�ա�PNC1����BM= ![]() ����C1M=MN-NC1=
����C1M=MN-NC1= ![]() ����Rt��PBE�У��ɹ��ɶ�������ã�PB=
����Rt��PBE�У��ɹ��ɶ�������ã�PB=![]() ������Rt��BMC1�У���BM2+C1M2=BC12���������ڡ�
������Rt��BMC1�У���BM2+C1M2=BC12���������ڡ�![]() ���ַ��̣��ⷽ����á�
���ַ��̣��ⷽ����á�![]() ����ֵ��������õ�C1�����ꣻͬ������õ�C2�����ꣻ����ϵ�C�ڵ�һ������һ�������ɵõ���C������.
����ֵ��������õ�C1�����ꣻͬ������õ�C2�����ꣻ����ϵ�C�ڵ�һ������һ�������ɵõ���C������.
���������
��1����ֱ��AB��y=��x+b��y���ڵ�A��0��4����
��b=4��
��ֱ��AB�ı���ʽΪ��y=��x+4.
����y=��x+4������y=0ʱ��x=4��
��ֱ��AB��x��Ľ���B������Ϊ��4��0����
��2���١���B������Ϊ��4��0����
��OB=4��
��ֱ��l��ֱƽ��OB��AB�ڵ�D����x���ڵ�E��
����D�ĺ�����Ϊ2��
����y=-x+4������x=2ʱ��y=-2+4=2��
����D��������2��2��.
��P��ֱ��l��һ���㣬���ڵ�D���Ϸ�����P��������Ϊn��
��PD=n-2��
��S��ABP=![]() PD��OB=
PD��OB=![]() ��
��
����S��ABP=8ʱ����![]() �����
����� ![]() ��
��
����ʱ��P������Ϊ��2��6����
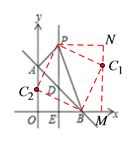
����ͼ�����C1��C2�Ƿ�������ĵ�C�����������ã��ı���BC1PC2�������Σ�����C1��C1M��x���ڵ�M������P��PN����MC1�ڵ�N�����ı���PEMN�Ǿ��Σ���C1MB�ա�PNC1��
��MN=PE=6��NC1=BM��PN=C1M=BM+BE��
��BM= ![]() ����C1M=MN-NC1=
����C1M=MN-NC1= ![]() .
.
����Rt��PBE��PE=6��BE=![]() OB=2��
OB=2��
��PB=![]() ��
��
����PB�ǵ���Rt��PC1B��б����
��BC1=![]() .
.
����Rt��BMC1��BM2+C1M2=BC12��
��![]() �������
������� ![]() ��
��
����![]() ʱ��PN=C1M=6-4=2<BM+BE��
ʱ��PN=C1M=6-4=2<BM+BE��
��![]() ֻ��ȡ2��
ֻ��ȡ2��
��BM=2��C1M=6-2=4��
��OM=OB+BM=4+2=6��
����C1��������6��4����
ͬ������õ�C2������Ϊ��0��2����
������C�ڵ�һ���ޣ�
����C��������6��4��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() �У�
�У�![]() Ϊ�����ε����
Ϊ�����ε����![]() �Ľ�ƽ���ߣ���
�Ľ�ƽ���ߣ���![]() ���߶�
���߶�![]() �ϣ�����
�ϣ�����![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ��������
��������![]() �ڵ�
�ڵ�![]() ��
��
��![]() ����ͼ1������
����ͼ1������![]() ���
���![]() �غϣ�
�غϣ�
�������ⲹȫͼ1��
���ж�![]() ��
��![]() ��������ϵ������֤����
��������ϵ������֤����
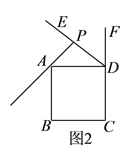
��![]() ����ͼ2������
����ͼ2������![]() ǡ�����߶�
ǡ�����߶�![]() �ϣ�������
�ϣ�������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ����д����
����д����![]() ����˼·�����Բ�д������������
����˼·�����Բ�д������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��E�ǡ�AOB��ƽ������һ�㣬EC��OB��ED��OA��C��D�Ǵ��㣬����CD���ҽ�OE�ڵ�F.
��1����֤��OE��CD�Ĵ�ֱƽ����.
��2������AOB=60������̽��OE��EF֮����ʲô������ϵ����֤����Ľ��ۡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Ǽ����ɨĹ�����ӣ����������������������������ʾ�����������ڼ�ȫ�м�ɨ������300���˴Σ����е�300���ÿ�ѧ��������ʾΪ�� ��
A.3��105
B.3��106
C.30��105
D.0.3��106
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��EF����O����AB��CD�ֱ��ཻ�ڵ�E��F������EC��
��1����֤��OE��OF��
��2����EF��AC����BEC���ܳ���10������ABCD���ܳ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������12�꣬���ְֽ���36�꣬�����ְֵ�������С�������2�������з��̲���������Ľ⣩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪������ͬһƽ���ڣ�����ֱ����һ������ֻ��һ��ֱ������ֱ֪��ƽ������

Сΰͬѧ��ͨ����ͬλ����ȣ���ֱ��ƽ��������ͼ�Σ����������ǣ�����P������һ��ֱ��a��ֱ��l�ཻ������PΪ������һ���ǣ�ֱ��aΪ�ǵ�һ������ֱ�ߣ���ǵ���һ������ֱ����ֱ��lƽ�У�
��1���������Сΰͬѧ���������������ʣ�����ͼ��������ͼ�ۼ�����д������
��2���㻹�������취�����ڱ���ͼ����ɣ�ֻ��һ�ּ��ɣ�������ͼ�ۼ�����д������


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������ε�ÿ����Ƕ�����45�㣬�������ڽǺ͵��ڣ� ��
A.720��
B.1040��
C.1080��
D.540��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����OC�ϵ�����һ�㵽��AOB�����ߵľ��붼��ȣ���D��E��F�ֱ�Ϊ��OC��OA��OB�ϣ����Ҫ��֤��OE=OF��ֻ��Ҫ���������ĸ������е�ijһ�����ɣ���д�����п��ܵ����������__________��
�١�ODE=��ODF���ڡ�OED=��OFD����ED=FD����EF��OC��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com