
【题目】如图所示,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE.
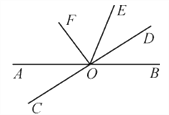
(1)判断OF与OD的位置关系;
(2)若∠AOC∶∠AOD=1∶5,求∠EOF的度数.
【答案】(1) OF⊥OD,理由见解析;(2) 60°.
【解析】试题分析:(1)根据角平分线的性质,可得![]() 与
与![]() 的关系,根据角的和差,可得
的关系,根据角的和差,可得![]() 的度数,可得答案;
的度数,可得答案;
(2)根据补角的性质, ![]() 可得
可得![]() 的度数,根据角的和差,可得
的度数,根据角的和差,可得![]() 的度数,根据角平分线的性质,可得答案.
的度数,根据角平分线的性质,可得答案.
试题解析:
(1)因为OF平分∠AOE,
所以∠AOF=∠EOF=![]() ∠AOE.
∠AOE.
又因为∠DOE=∠BOD=![]() ∠BOE,
∠BOE,
所以∠DOE+∠EOF=![]() (∠BOE+∠AOE)=
(∠BOE+∠AOE)= ![]() ×180°=90°,
×180°=90°,
即∠FOD=90°.
所以OF⊥OD.
(2)设∠AOC=x°,
因为∠AOC∶∠AOD=1∶5,
所以∠AOD=5x°.
因为∠AOC+∠AOD=180°,
所以x+5x=180,x=30.
所以∠DOE=∠BOD=∠AOC=30°.
又因为∠FOD=90°,
所以∠EOF=90°-30°=60°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=45°,则∠ACB的度数为 ;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国的陆地面积约为9600000km2 , 将这个数用科学记数法可表示为( )
A.0.96×107km2
B.960×104km2
C.9.6×106km2
D.9.6×105km2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A.两人同时出发,各自到达终点后停止.设两人之间的距离为s(千米),甲行驶的时间为t(小时),则下图中正确反映s与t之间函数关系的是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】( 2017大连)在平面直角坐标系xOy中,线段AB的两个端点坐标分别为A(﹣1,﹣1),B(1,2),平移线段AB,得到线段A′B′,已知A′的坐标为(3,﹣1),则点B′的坐标为( )
A.(4,2)
B.(5,2)
C.(6,2)
D.(5,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为4的正方形OABC置于平面直角坐标系中,点P在边OA上从O向A运动,连接CP交对角线OB于点Q,连接AQ. 
(1)求证:△OCQ≌△OAQ;
(2)当点Q的坐标为( ![]() ,
, ![]() )时,求点P的坐标;
)时,求点P的坐标;
(3)若点P在边OA上从点O运动到点A后,再继续在边AB上从A运动到点B,在整个过运动过程中,若△OCQ恰为等腰三角形,请直接写出所有满足条件的点P的坐标. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com