
【题目】如图,将边长为4的正方形OABC置于平面直角坐标系中,点P在边OA上从O向A运动,连接CP交对角线OB于点Q,连接AQ. 
(1)求证:△OCQ≌△OAQ;
(2)当点Q的坐标为( ![]() ,
, ![]() )时,求点P的坐标;
)时,求点P的坐标;
(3)若点P在边OA上从点O运动到点A后,再继续在边AB上从A运动到点B,在整个过运动过程中,若△OCQ恰为等腰三角形,请直接写出所有满足条件的点P的坐标. 
【答案】
(1)证明:∵四边形OCBA是正方形,
∴OC=OA,∠COD=∠AOD=45°,
在△OCD和△OAD中 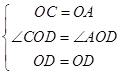 ,
,
∴△OCD≌△OAD(SAS),
(2)解:∵点Q的坐标为( ![]() ,
, ![]() ),
),
∴OQ= ![]() ,
,
在正方形OABC中,BC∥OA,OC=BC=4,
∴OB=4 ![]() ,
,
∴BQ=OB﹣OQ= ![]() ,
,
∵BC∥OA,
∴△OQP∽△BQC,
∴ ![]() ,
,
∴ 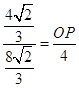 ,
,
∴OP=2,
∴P(2,0);
(3)解:解:分为三种情况:
①OC=OD时,如图1,
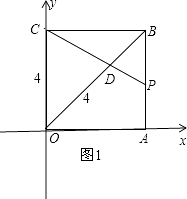
∴OD=4,
∵OB=4 ![]() ,
,
∴BD=OB﹣OD=4 ![]() ﹣4,
﹣4,
∵∠BOC=45°,
∴∠OCP=67.5°,
∴点P在AB上,
∵OC∥AB,
∴△ODC∽△BDP,
∴ ![]() ,
,
∴ ![]() ,
,
∴BP=4 ![]() ﹣4,
﹣4,
∴AP=AB﹣BP=4﹣(4 ![]() ﹣4)=8﹣4
﹣4)=8﹣4 ![]() ,
,
∴P点的坐标是(4,8﹣4 ![]() );
);
②CD=OD时,如图2,
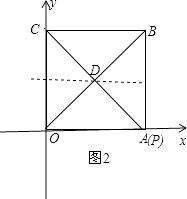
∵∠BOC=45°,
∴点D是OB的中点,
∴点P与点A重合,
∴P点的坐标是(4,0);
③OC=CD时,
∴∠CDO=∠COD=45°.
∴∠OCD=90°,
∴点P和点B重合,
∴P点的坐标是(4,4).
即满足条件的点P的坐标为(4,8﹣4 ![]() )或(4,0)或(4,4).
)或(4,0)或(4,4).
【解析】(1)根据正方形性质推出OC=OA,∠COD=∠AOD=45°,根据SAS证明三角形全等即可;(2)先求出OB,OQ,进而判断出△OQP∽△BQC,即可得出结论.(3)分为三种情况:①OC=OD时,②CD=OD时,③OC=CD时,根据等腰三角形性质和相似求出即可.
【考点精析】本题主要考查了等腰三角形的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图所示,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE.
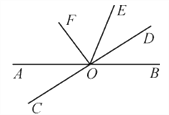
(1)判断OF与OD的位置关系;
(2)若∠AOC∶∠AOD=1∶5,求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图所示,则①
的图象如图所示,则①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤4a+2b+c>0;⑥a+b+c>0上述六个结论中正确的有( )
;⑤4a+2b+c>0;⑥a+b+c>0上述六个结论中正确的有( )

A. 两个 B. 三个 C. 四个 D. 五个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业的年收入约为700000元,数据“700000”用科学记数法可表示为( )
A.0.7×106
B.7×105
C.7×104
D.70×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用同样规格的黑白两色的正方形瓷砖铺设矩形地面,请观察下列图形并解答有关问题.
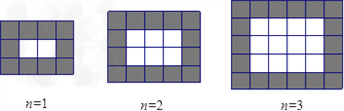
(1)在第n个图中,第一横行共_________ 块瓷砖,第一竖列共有_________ 块瓷砖;(均用含n的代数式表示)
(2)设铺设地面所用瓷砖的总块数为y,请写出y与(1)中的n的函数关系式;
(3)按上述铺设方案,铺一块这样的矩形地面共用了506块瓷砖,求此时n的值;
(4)黑瓷砖每块4元,白瓷砖每块3元,问题(3)中,共花多少元购买瓷砖;
(5)是否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在AB上.
(1)试找出∠1,∠2,∠3之间的关系并说出理由;
(2)如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com