
����Ŀ����ͼ����ͬ�����ĺڰ���ɫ�������δ�ש������ε��棬��۲�����ͼ�β�����й����⣮
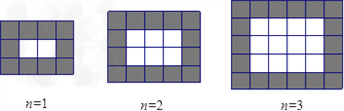
��1���ڵ�n��ͼ�У���һ���й�_________ ���ש����һ���й���_________ ���ש�������ú�n�Ĵ���ʽ��ʾ��
��2��������������ô�ש���ܿ���Ϊy����д��y�루1���е�n�ĺ�����ϵʽ��
��3�����������跽������һ�������ľ��ε��湲����506���ש�����ʱn��ֵ��
��4���ڴ�שÿ��4Ԫ���״�שÿ��3Ԫ�����⣨3���У���������Ԫ�����ש��
��5���Ƿ���ںڴ�ש��״�ש������ȵ����Σ���ͨ������˵�����ɣ�
���𰸡���1����n+3������n+2������2��y=��n+3����n+2������3��20����4��1604Ԫ����5�������ڣ����ɲμ�������
�������������������1���۲�ͼ�Σ��ҳ����ɼ��ɣ���2����1��ͼ����4��3���ש����2��ͼ����5��4���ש����3��ͼ����6��5���ש�����Կ����Ƴ���ש���ܿ���Ϊy=��n+3����n+2������3����y=506ʱ���Դ��루1���к�����ϵʽ���n����4���ͣ�1��һ�������Ƴ��״�ש���ܿ���Ϊy'= n��n+1����Ȼ������Ƴ��ڴ�ש��Ŀ���ٸ�����֪�������ɼ����Ǯ������5�����ã�4���Ľ��ۼ��㼴���ж��Ƿ���ڣ�
�����������1���۲�ͼ�ε�֪����n=1ʱ������Ϊ1+3=4�飬������1+2=3�飬��n=2ʱ������Ϊ2+3=5�飬������2+2=4�飬��n=3ʱ������Ϊ3+3=6�飬������3+2=5�飬�������ÿ�������У�n+3���飬ÿ�������У�n+2���飮��2����n=1ʱ��y=��1+3����1+2��=12����n=2ʱ��y=��2+3����2+2��=20����n=3ʱ��y=��3+3����3+2��=30������y��n�ĺ�����ϵʽΪ��y=��n+3����n+2������3�������⣬�ã�n+3����n+2��=506�������ã�n2+5n-500=0����ã�n=![]() ����n1=20��n2=��25����ȥ��������n��ֵΪ20����4���۲�ͼ�ο�֪��ÿ�������а�ש��n+1���飬ÿ�������а�שn�飬�����ש������n��n+1���飬n=20ʱ����שΪ20��21=420���飩����ש��Ϊ506��420=86���飩������Ǯ��Ϊ420��3+86��4=1260+344=1604��Ԫ������5���ڰ�ש����Ϊ��n+2����n+3��=n2+5n+6�����ڰ�ש�������ʱ���з���n��n+1��=��n2+5n+6����n��n+1����������n2��3n��6=0����֮��n1=
����n1=20��n2=��25����ȥ��������n��ֵΪ20����4���۲�ͼ�ο�֪��ÿ�������а�ש��n+1���飬ÿ�������а�שn�飬�����ש������n��n+1���飬n=20ʱ����שΪ20��21=420���飩����ש��Ϊ506��420=86���飩������Ǯ��Ϊ420��3+86��4=1260+344=1604��Ԫ������5���ڰ�ש����Ϊ��n+2����n+3��=n2+5n+6�����ڰ�ש�������ʱ���з���n��n+1��=��n2+5n+6����n��n+1����������n2��3n��6=0����֮��n1=![]() ��n2=
��n2=![]() ������n1��ֵ����������n2��ֵ�Ǹ������ʲ����ںڰ�ש������ȵ����Σ�
������n1��ֵ����������n2��ֵ�Ǹ������ʲ����ںڰ�ש������ȵ����Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��B�������120ǧ�ף��������г���20ǧ��/ʱ���ٶ������Aǰ���յ�B������Ħ�г���40ǧ��/ʱ���ٶ������Bǰ���յ�A������ͬʱ���������Ե����յ��ֹͣ��������֮��ľ���Ϊs��ǧ�ף�������ʻ��ʱ��Ϊt��Сʱ��������ͼ����ȷ��ӳs��t֮�亯����ϵ���ǣ� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���B�������ǣ�4����1������A���B����x��Գƣ����A�������ǣ�������
A. ��4��1�� B. ����1��4�� C. ����4����1�� D. ����1����4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߳�Ϊ4��������OABC����ƽ��ֱ������ϵ�У���P�ڱ�OA�ϴ�O��A�˶�������CP���Խ���OB�ڵ�Q������AQ�� 
��1����֤����OCQ�ա�OAQ��
��2������Q�������� ![]() ��
�� ![]() ��ʱ�����P�����ꣻ
��ʱ�����P�����ꣻ
��3������P�ڱ�OA�ϴӵ�O�˶�����A���ټ����ڱ�AB�ϴ�A�˶�����B�����������˶������У�����OCQǡΪ���������Σ���ֱ��д���������������ĵ�P�����꣮ 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC���ܳ�Ϊ1�����ӡ�ABC�������е㹹�ɵڶ��������Σ������ӵڶ��������ε������е㹹�ɵ����������Σ��������ƣ���2010�������ε��ܳ��ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У��ѵ�P����5��4������ƽ��9����λ�õ���P1���ٽ���P1��ԭ��˳ʱ����ת90���õ���P2�����P2�������ǣ�������
A. ��4����4�� B. ��4��4�� C. ����4����4�� D. ����4��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���BAD����ACB��90����AB��AD��AC��4BC����CD�ij�Ϊx���ı���ABCD�����Ϊy����y��x֮��ĺ�������ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�ǵȱ������Σ�D��BC���ϵ�һ�����㣨��D����B��C�غϣ���ADF����ADΪ�ߵĵȱ������Σ�����F��BC��ƽ���߽�����AC�ڵ�E������BF��
��1����ͼ1����֤����AFB�ա�ADC�� 
��2�����ж�ͼ1���ı���BCEF����״����˵�����ɣ�
��3����D����BC �ߵ��ӳ����ϣ���ͼ2�������������䣬���ʣ�2���н��ۻ������������������˵�����ɣ� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ABΪ��O��ֱ����AB=AC��BC����O�ڵ�D��AC����O�ڵ�E����BAC=45�ȣ���������������ۣ�����EBC=22.5�㣻��BD=DC����AE=2EC�����ӻ�AE���ӻ�DE��2������AE=BC��������ȷ���۵�����ǣ�������
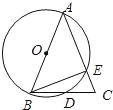
A. �٢ڢ� B. �٢ڢ� C. �٢ڢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com