
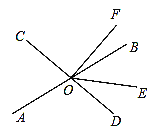
【题目】直线AB、CD相交于点O,OE平分∠BOD.OF⊥CD,垂足为O,若∠EOF=54°.
(1)求∠AOC的度数;
(2)作射线OG⊥OE,试求出∠AOG的度数.
【答案】(1)72°(2)54°或126°
【解析】
(1)依据垂线的定义,即可得到∠DOE的度数,再根据角平分线的定义,即可得到∠BOD的度数,进而得出结论;
(2)分两种情况讨论,依据垂线的定义以及角平分线的定义,即可得到∠AOG的度数.
(1)∵OF⊥CD,∠EOF=54°,
∴∠DOE=90°﹣54°=36°,
又∵OE平分∠BOD,
∴∠BOD=2∠DOE=72°,
∴∠AOC=72°;
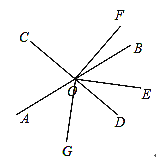
(2)如图,若OG在∠AOD内部,则
由(1)可得,∠BOE=∠DOE=36°,
又∵∠GOE=90°,
∴∠AOG=180°﹣90°﹣36°=54°;
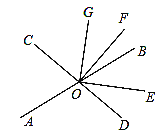
如图,若OG在∠COF内部,则
由(1)可得,∠BOE=∠DOE=36°,
∴∠AOE=180°﹣36°=144°,
又∵∠GOE=90°,
∴∠AOG=360°﹣90°﹣144°=126°.
综上所述,∠AOG的度数为54°或126°.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在5×5的正方形网格中,每个小正方形的边长均为1,线段AB的端点在格点上,按要求画出格点三角形,并求其面积.
(1)在图①中画出一个以 AB为腰的等腰三角形 ABC,其面积为____________.
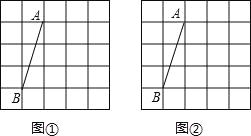
(2) 在图②中画出一个以AB为底的等腰三角形ABC,其面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为6cm,点E、M分别是线段BD、AD上的动点,连接AE并延长,交边BC于F,过M作MN⊥AF,垂足为H,交边AB于点N.
(1)如图1,若点M与点D重合,求证:AF=MN;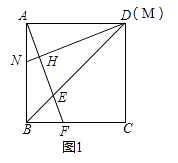
(2)如图2,若点M从点D出发,以1cm/s的速度沿DA向点A运动,同时点E从点B出发,以 ![]() cm/s的速度沿BD向点D运动,运动时间为t s.
cm/s的速度沿BD向点D运动,运动时间为t s.
①设BF=y cm,求y关于t的函数表达式;
②当BN=2AN时,连接FN,求FN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE.
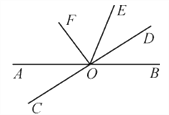
(1)判断OF与OD的位置关系;
(2)若∠AOC∶∠AOD=1∶5,求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠BOM=90°,∠DON=90°.
(1)若∠COM=∠AOC,求∠AOD的度数;
(2)若∠COM=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.

查看答案和解析>>
科目:初中数学 来源: 题型:
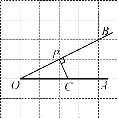
【题目】如图,点P是∠AOB的边OB上的一点,过点P画OB的垂线,交OA于点C.
(1)过点P画OA的垂线,垂足为H;
(2)线段PH的长度是点P到____的距离,____是点C到直线OB的距离.线段PC,PH,OC这三条线段大小关系是___.(用“<”号连接)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD.
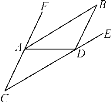
(1)判断∠FAB与∠C的大小关系,请说明理由;
(2)若∠C=35°,AB是∠FAD的平分线.
①求∠FAD的度数;
②若∠ADB=110°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
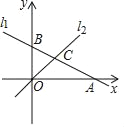
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家庭过期药品属于“国家危险废物“处理不当将污染环境,危害健康。某市药监部门为了了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调查
(1)下列选取样本的方法最合理的一种是(只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;
②在全市医务工作者中以家庭为单位随机抽取③在全市常住人口中以家庭为单位随机抽取.
(2)本次抽样调查发现,接受调查的家庭都有过期药品,现将有关数据呈现如下图: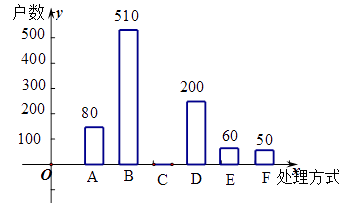
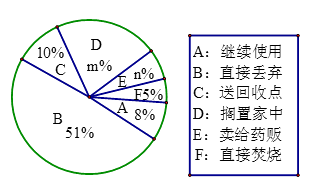
①求m、n的值.
②补全条形统计图
③根据调查数据,你认为该市市民家庭处理过期药品最常见的方式是什么?
④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收点。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com