
【题目】如图,已知AB∥CD.
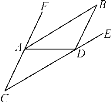
(1)判断∠FAB与∠C的大小关系,请说明理由;
(2)若∠C=35°,AB是∠FAD的平分线.
①求∠FAD的度数;
②若∠ADB=110°,求∠BDE的度数.
【答案】(1)∠FAB=∠C;(2) ①∠FAD=70°;②∠BDE=35°
【解析】
(1)相等,根据平行线的性质由AB∥CD,得到∠FAB=∠C即可;
(2)①根据角平分线的定义得到∠FAD=2∠FAB,代入求出即可;
②求出∠ADB+∠FAD=180°,根据平行线的判定得出CF∥BD,再根据平行线的性质推出∠BDE=∠C=35°.
(1)∠FAB与∠C的大小关系是相等,
理由是:∵AB∥CD,
∴∠FAB=∠C.
(2)①∵∠FAB=∠C=35°,
∵AB是∠FAD的平分线,
∴∠FAD=2∠FAB=2×35°=70°,
答:∠FAD的度数是70°.
②∵∠ADB=110°,∠FAD=70°,
∴∠ADB+∠FAD=110°+70°=180°,
∴CF∥BD,
∴∠BDE=∠C=35°,
答:∠BDE的度数是35°.


科目:初中数学 来源: 题型:
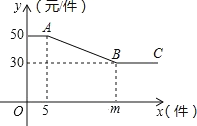
【题目】某商店经销某种玩具,该玩具每个进价 20 元,为进行促销,商店制定如下“优惠” 方案:如果一次销售数量不超过 5 个,则每个按 50 元销售:如果一次销售数量超过 5 个,则每增加一个,所有玩具均降低 1 元销售,但单价不得低于 30 元,一次销售该玩具的单价 y(元)与销售数量 x(个)之间的函数关系如下图所示.
(1)结合图形,求出 m 的值;射线 BC 所表示的实际意义是什么;
(2)求线段 AB 满足的 y 与 x 之间的函数解析式,并直接写出自变量的取值范围;
(3)当销售 15 个时,商店的利润是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
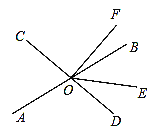
【题目】直线AB、CD相交于点O,OE平分∠BOD.OF⊥CD,垂足为O,若∠EOF=54°.
(1)求∠AOC的度数;
(2)作射线OG⊥OE,试求出∠AOG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形EFGH四个顶点分别在菱形ABCD的四条边上,BE=BF,将△AEH,△CFG分别沿边EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的 ![]() 时,则
时,则 ![]() 为( )
为( )
A.![]()
B.2
C.![]()
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10m.拴住小狗的10m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2).
①如图1,若BC=4m,则S=m.
②如图2,现考虑在(1)中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其它条件不变.则在BC的变化过程中,当S取得最小值时,边BC的长为m.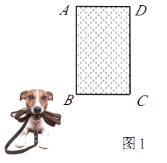
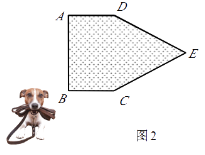
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次测绘活动中,某同学站在点A处观测停放于B、C两处的小船,测得船B在点A北偏东75°方向150米处,船C在点A南偏东15°方向120米处,则船B与船C之间的距离为______米(精确到0.1![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:已知a+b=﹣4,ab=3,求a2+b2的值.
解:∵a+b=﹣4,ab=3,
∴a2+b2=(a+b)2﹣2ab=(﹣4)2﹣2×3=10.
请你根据上述解题思路解答下面问题:
(1)已知a﹣b=﹣3,ab=﹣2,求(a+b)(a2﹣b2)的值.
(2)已知a﹣c﹣b=﹣10,(a﹣b)c=﹣12,求(a﹣b)2+c2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com