
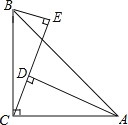
【题目】如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
(1)求证:△ACD≌△CBE;
(2)若AD=12,DE=7,求BE的长.
【答案】(1)证明见解析;(2)BE=5.
【解析】
(1)根据垂直定义求出∠BEC=∠ACB=∠ADC,根据等式性质求出∠ACD=∠CBE,根据AAS证明△BCE≌△CAD;
(2)根据全等三角形的对应边相等得到AD=CE,CD=BE,再根据AD=12,DE=7,即可解答.
(1)∵∠ACB=90°,BE⊥CE,
∴∠ECB+∠ACD=90°∠ECB+∠CBE=90°,
∴∠ACD=∠CBE,
∵AD⊥CE,BE⊥CE,
∴∠ADC=∠CEB=90°,
∵AC=BC,
∴△ACD≌△CBE;
(2)∵△ACD≌△CBE,
∴AD=CE,CD=BE,
∵AD=12,DE=7,
∴BE=CD=CE-DE=12-7=5.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】(1)如图,平移三角形ABC,使点A平移到点![]() ,画出平移后的三角形
,画出平移后的三角形![]() ;
;
(2)在(1)的条件下,指出点A,B,C 的对应点,并指出AB,BC,AC的对应线段和∠A,∠B, ∠C的对应角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为节约水资源,制定了新的居民用水收费标准,按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示. 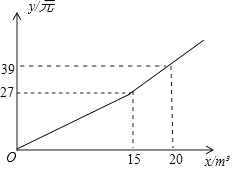
(1)求y关于x的函数解析式;
(2)若某用户二、三月份共用水40cm3(二月份用水量不超过25cm3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b(k≠0)与双曲线y= ![]() (m≠0)相交于A(1,2),B(n,﹣1)两点.
(m≠0)相交于A(1,2),B(n,﹣1)两点. 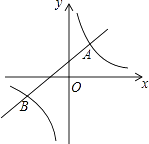
(1)求双曲线的解析式;
(2)若A1(x1 , y1),A2(x2 , y2),A3(x3 , y3)为双曲线上的三点,且x1<0<x2<x3 , 请直接写出y1 , y2 , y3的大小关系;
(3)观察图象,请直接写出不等式kx+b< ![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件
B.审查书稿中有哪些学科性错误适合用抽样调查法
C.甲乙两人在相同条件下各射击10次,他们的成绩的平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定
D.掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多好佳水果店在批发市场购买某种水果销售,第一次用1500元购进若干千克,并以每千克9元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1694元所购买的水果比第一次多20千克,以每千克10元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价45%售完剩余的水果.
(1)第一次水果的进价是每千克多少元?
(2)该水果店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
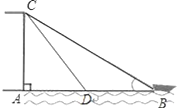
【题目】已知:如图,有人在岸上点C的地方,用绳子拉船靠岸,开始时,绳长CB=10米,CA⊥AB,且CA=6米,拉动绳子将船从点B沿BA方向行驶到点D后,绳长CD=6![]() 米.
米.
(1)试判定△ACD的形状,并说明理由;
(2)求船体移动距离BD的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生课外阅读的喜好,某校从八年级随机抽取部分学生进行问卷调查,调查要求每人只选取一种喜欢的书籍,如果没有喜欢的书籍,则作“其它”类统计。图(1)与图(2)是整理数据后绘制的两幅不完整的统计图。以下结论不正确的是( )
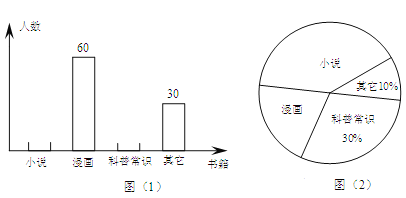
A. 由这两个统计图可知喜欢“科普常识”的学生有90人.
B. 若该年级共有1200名学生,则由这两个统计图可估计喜爱“科普常识”的学生约有360个.
C. 由这两个统计图不能确定喜欢“小说”的人数.
D. 在扇形统计图中,“漫画”所在扇形的圆心角为72°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一串有理数按下列规律排列,回答下列问题.

(1)在A处的数是正数还是负数?
(2)负数排在A、B、C、D中的什么位置?
(3)第2 015个数是正数还是负数?排在对应于A、B、C、D中的什么位置?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com