
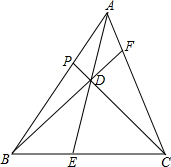
 如图,在△ABC中,设E,F,P分别在边BC,CA,AB上,已知AE,BF,CP交于一点D,且$\frac{AD}{DE}$+$\frac{BD}{DF}$+$\frac{CD}{DP}$=n,则$\frac{AD}{DE}$$•\frac{BD}{DF}•\frac{CD}{DP}$=n+2.
如图,在△ABC中,设E,F,P分别在边BC,CA,AB上,已知AE,BF,CP交于一点D,且$\frac{AD}{DE}$+$\frac{BD}{DF}$+$\frac{CD}{DP}$=n,则$\frac{AD}{DE}$$•\frac{BD}{DF}•\frac{CD}{DP}$=n+2. 分析 设S△BCD=S1,S△CAD=S2,S△ABD=S3,根据等高三角形的面积的比等于底的比得到$\frac{AD}{DE}$═$\frac{{S}_{3}{+S}_{2}}{{S}_{1}}$,同理$\frac{BD}{DF}=\frac{{S}_{1}{+S}_{3}}{{S}_{2}}$,$\frac{CD}{DP}=\frac{{S}_{1}{+S}_{2}}{{S}_{3}}$,于是得到n+2=$\frac{{S}_{3}{+S}_{2}}{{S}_{1}}$+$\frac{{S}_{1}{+S}_{3}}{{S}_{2}}$+$\frac{{S}_{1}{+S}_{2}}{{S}_{3}}$+2,通过化简得到$\frac{({S}_{1}+{S}_{2})({S}_{1}+{S}_{3})({S}_{2}+{S}_{3})}{{S}_{1}{S}_{3}{S}_{2}}$,从而得到$\frac{AD}{DE}$$•\frac{BD}{DF}•\frac{CD}{DP}$=$\frac{({S}_{1}+{S}_{2})({S}_{1}+{S}_{3})({S}_{2}+{S}_{3})}{{S}_{1}{S}_{3}{S}_{2}}$=n+2.
解答 解:设S△BCD=S1,S△CAD=S2,S△ABD=S3,
∴$\frac{AD}{DE}$=$\frac{{S}_{△ABD}}{{S}_{△EBD}}$=$\frac{{S}_{△ACD}}{{S}_{△ECD}}$=$\frac{{S}_{△ABD}{+S}_{△ACD}}{{S}_{△EBD}{+S}_{△ECD}}$=$\frac{{S}_{3}{+S}_{2}}{{S}_{1}}$,
同理$\frac{BD}{DF}=\frac{{S}_{1}{+S}_{3}}{{S}_{2}}$,$\frac{CD}{DP}=\frac{{S}_{1}{+S}_{2}}{{S}_{3}}$,
∴n+2=$\frac{{S}_{3}{+S}_{2}}{{S}_{1}}$+$\frac{{S}_{1}{+S}_{3}}{{S}_{2}}$+$\frac{{S}_{1}{+S}_{2}}{{S}_{3}}$+2
=$\frac{{{S}_{2}S}_{3}{(S}_{2}{+S}_{3}){{+S}_{1}S}_{3}{(S}_{1}{+S}_{3})}{{{{S}_{1}S}_{2}S}_{3}}$+$\frac{{{S}_{1}S}_{2}{(S}_{1}{+S}_{2})+{{{2S}_{1}S}_{2}S}_{3}}{{S}_{1}{S}_{2}{S}_{3}}$
=$\frac{{S}_{2}{{S}_{3}}^{2}+{{S}_{2}}^{2}{S}_{3}+{{S}_{1}}^{2}{S}_{3}+{S}_{1}{{S}_{3}}^{2}}{{S}_{1}{S}_{2}{S}_{3}}$+$\frac{{{S}_{1}}^{2}{S}_{2}{+S}_{1}{{S}_{2}}^{2}+2{S}_{1}{S}_{2}{S}_{3}}{{S}_{1}{S}_{2}{S}_{3}}$
=$\frac{({{S}_{1}}^{2}{S}_{2}+{{S}_{1}}^{2}{S}_{3}+{S}_{1}{S}_{2}{S}_{3}+{S}_{1}{{S}_{3}}^{2})}{{S}_{1}{S}_{2}{S}_{3}}$+$\frac{({S}_{1}{{S}_{2}}^{2}+{S}_{1}{S}_{2}{S}_{3}+{{S}_{2}}^{2}{S}_{3}+{S}_{2}{{S}_{3}}^{2})}{{S}_{1}{S}_{2}{S}_{3}}$
=$\frac{{S}_{1}({S}_{1}{S}_{2}+{S}_{1}{S}_{3}+{S}_{2}{S}_{3}+{{S}_{3}}^{2})}{{S}_{1}{S}_{2}{S}_{3}}$+$\frac{{S}_{2}({S}_{1}{S}_{2}+{S}_{1}{S}_{3}+{S}_{2}{S}_{3}{{+S}_{3}}^{2})}{{S}_{1}{S}_{2}{S}_{3}}$
=$\frac{{S}_{1}({S}_{1}+{S}_{3})({S}_{2}+{S}_{3})+{S}_{2}({S}_{1}+{S}_{3})({S}_{2}+{S}_{3})}{{S}_{1}{S}_{2}{S}_{3}}$
=$\frac{({S}_{1}+{S}_{2})({S}_{1}+{S}_{3})({S}_{2}+{S}_{3})}{{S}_{1}{S}_{3}{S}_{2}}$,
∴$\frac{AD}{DE}$$•\frac{BD}{DF}•\frac{CD}{DP}$=$\frac{({S}_{1}+{S}_{2})({S}_{1}+{S}_{3})({S}_{2}+{S}_{3})}{{S}_{1}{S}_{3}{S}_{2}}$=n+2.
故答案为:n+2.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了坐标与图形性质.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
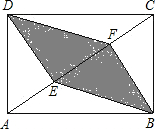 如图,一块矩形场地ABCD,现测得边长AB与AD之比为$\sqrt{2}$:1,DE⊥AC于点E,BF⊥AC于点F,连接BE,DF.现计划在四边形DEBF区域内种植花草.
如图,一块矩形场地ABCD,现测得边长AB与AD之比为$\sqrt{2}$:1,DE⊥AC于点E,BF⊥AC于点F,连接BE,DF.现计划在四边形DEBF区域内种植花草.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com