
【题目】把几个数用大括号围起来,中间用逗号断开,如:{1,2,﹣3}、{﹣2,7,![]() ,19},我们称之为集合,其中的每个数称为该集合的元素.如果一个所有元素均为有理数的集合满足:当有理数a是集合的元素时,2015﹣a也必是这个集合的元素,这样的集合我们称为好的集合.例如集合{2015,0}就是一个好的集合.
,19},我们称之为集合,其中的每个数称为该集合的元素.如果一个所有元素均为有理数的集合满足:当有理数a是集合的元素时,2015﹣a也必是这个集合的元素,这样的集合我们称为好的集合.例如集合{2015,0}就是一个好的集合.
(1)集合{2015}_____好的集合,集合{﹣1,2016}_____好的集合(两空均填“是”或“不是”);
(2)若一个好的集合中最大的一个元素为4011,则该集合是否存在最小的元素?如果存在,请直接写出答案,否则说明理由;
(3)若一个好的集合所有元素之和为整数M,且22161<M<22170,则该集合共有几个元素?说明你的理由.
【答案】不是是
【解析】
(1)根据有理数a是集合的元素时,2015-a也必是这个集合的元素,这样的集合我们称为好的集合,从而可以可解答本题;
(2)根据2015-a,如果a的值越大,则2015-a的值越小,从而可以解答本题;
(3)根据题意可知好的集合都是成对出现的,并且这对对应元素的和为2015,然后通过估算即可解答本题.
解:(1)根据题意可得20152015=0,而集合{2015}中没有元素0,故{2015}不是好的集合;
∵2015(1)=2016,20152016=1,
∴集合{1,2016}是好的集合.
故答案为:不是,是.
(2)一个好的集合中最大的一个元素为4001,则该集合存在最小的元素,该集合最小的元素是1986.
∵2015a中a的值越大,则2015a的值越小,
∴一个好的集合中最大的一个元素为4001,则最小的元素为:20154001=1986.
(3)该集合共有22个元素.
理由:∵在好的集合中,如果一个元素为a,则另一个元素为2015a,
∴好的集合中的元素一定是偶数个.
∵好的集合中的每一对对应元素的和为:a+2015a=2015,2015×11=22165,2015×10=20150,2015×12=24180,
又∵一个好的集合所有元素之和为整数M,且22161<M<22170,
∴这个好的集合中的元素个数为:11×2=22个.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】如图,在平整的地面上,用若干个棱长完全相同的小正方体堆成一个几何体.
(1)请画出这个几何体的三视图.
(2)如果现在你手头还有一些相同的小正方体,要求保持俯视图和左视图不变,最多可以再添加几个小正方体


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,∠MAC=∠CAB,作CD⊥AM,垂足为D. 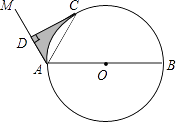
(1)求证:CD是⊙O的切线;
(2)若∠ACD=30°,AD=4,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产1 400辆自行车,平均每天生产200辆.由于各种原因,实际上每天的生产量与计划量相比有出入.表是某周的生产情况(增产为正,减产为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | +5 | ﹣2 | ﹣4 | +13 | ﹣10 | +16 | ﹣9 |
(1)根据记录的数据可知该厂星期五生产自行车 辆;
(2)产量最多的一天比产量最少的一天多生产了 辆自行车;
(3)根据记录的数据可知该厂本周实际生产自行车 辆;
(4)该厂实行计件工资制,每生产一辆得60元,超额完成则每辆奖15元,少生产一辆则扣15元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果保留根号)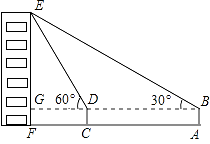
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.例如正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.
(1)如果⊙P是以(3,4)为圆心,1为半径的圆,那么点O(0,0)到⊙P的距离为
(2)求点 ![]() 到直线
到直线 ![]() 的距离;
的距离;
(3)如果点 ![]() 到直线
到直线 ![]() 的距离为3,求a的值.
的距离为3,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线 ![]() (
( ![]() <
< ![]() <0)与x轴最多有一个交点,现有以下结论:
<0)与x轴最多有一个交点,现有以下结论:
① ![]() <0;②该抛物线的对称轴在y轴左侧;③关于x的方程
<0;②该抛物线的对称轴在y轴左侧;③关于x的方程 ![]() 有实数根;④对于自变量x的任意一个取值,都有
有实数根;④对于自变量x的任意一个取值,都有 ![]() ,其中正确的为( )
,其中正确的为( )
A.①②
B.①②④
C.①②③
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在已知线段AB的同侧构造∠FAB=∠GBA,并且在射线AF,BG上分别取点D和E,在线段AB上取点C,连结DC和EC.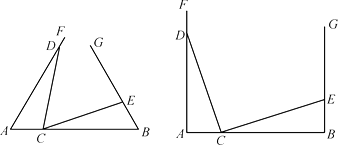
Ⅰ、如图,若AD=3,BE=1,△ADC≌△BCE.在∠FAB=∠GBA=60或∠FAB=∠GBA=90两种情况中任选一种,解决以下问题:
①线段AB的长度是否发生变化,直接写出长度或变化范围;
②∠DCE的度数是否发生变化,直接写出度数或变化范围.
Ⅱ、若AD=a,BE=b,∠FAB=∠GBA=α,且△ADC和△BCE这两个三角形全等,请求出:
①线段AB的长度或取值范围,并说明理由;
②∠DCE的度数或取值范围,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置. 
(1)旋转中心是点 , 旋转角度是度;
(2)若连结EF,则△AEF是三角形;并证明;
(3)若四边形AECF的面积为25,DE=2,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com