
【题目】设点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.例如正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.
(1)如果⊙P是以(3,4)为圆心,1为半径的圆,那么点O(0,0)到⊙P的距离为
(2)求点 ![]() 到直线
到直线 ![]() 的距离;
的距离;
(3)如果点 ![]() 到直线
到直线 ![]() 的距离为3,求a的值.
的距离为3,求a的值.
【答案】
(1)4
(2)
解:直线 ![]() 记为
记为 ![]() ,过点
,过点 ![]() 作
作 ![]() ,垂足为点
,垂足为点 ![]() ,
,
设 ![]() 与
与 ![]() 轴的交点分别为
轴的交点分别为 ![]() ,则
,则 ![]() .
.
∴ ![]() .
.
∵ ![]()
∴ ![]() ,即
,即 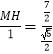 .∴
.∴ ![]() .
.
∴点 ![]() 到直线
到直线 ![]() 的距离为
的距离为 ![]() .
.
(3)
![]()
【解析】(1)OP=![]() =5,
=5,
点O(0,0)到⊙P的距离为5-1=4;
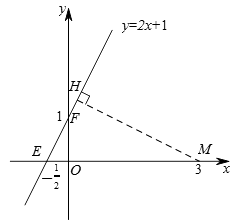
(2)直线 y = 2 x + 1 记为 l ,过点 M 作 M H ⊥ l ,垂足为点 H ,
设 ![]() 与
与 ![]() 轴的交点分别为
轴的交点分别为 ![]() ,则
,则 ![]() .
.
图1
∴ ![]() .
.
∵ ![]()
∴ ![]() ,即
,即 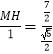 .∴
.∴ ![]() .
.
∴点 ![]() 到直线
到直线 ![]() 的距离为
的距离为 ![]() .
.
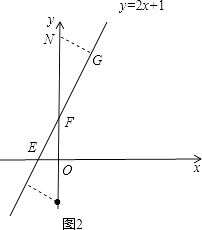
(3)②N在F点的上边,如图2,过点N作NG⊥l,垂足为点G,
∵△EOF∽△NGF,
∴![]() =
=![]() ,
,
即![]()
![]() ,
,
∴a=1+3![]() ;
;
N在F点的下边,
同理可得a=1-3![]() ;
;
故a=1±3![]() .
. 
(1)根据勾股定理可得点O(0,0)到⊙P的距离;
(2)过点M作MH⊥l,垂足为点H,通过证明△EOF∽△MHE,由相似三角形的性质可得MH , 从而得到点M到直线y=2x+1的距离;
(3)分两种情况:N在F点的上边;N在F点的下边;进行讨论先得到EN的长,进一步即可得到a的值.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源: 题型:
【题目】在股市交易中,每买、卖一次需付交易款的千分之七点五作为交易费用,某投资者以每股10元的价格买入某股票1 000股,下表为第一周内每日该股票的涨跌情况(单位:元).
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 | +2 | +1.5 | -0.5 | -4.5 | +2.5 |
(1)星期三收盘时,每股是多少元?
(2)本周内每股最高价是多少元?最低价是多少元?
(3)若该投资者在星期五收盘前将股票全部卖出,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.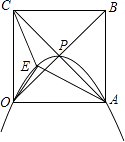
(1)建立适当的平面直角坐标系,
①直接写出O、P、A三点坐标;
②求抛物线L的解析式;
(2)求△OAE与△OCE面积之和的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数y= ![]() (x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).则点F的坐标是
(x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).则点F的坐标是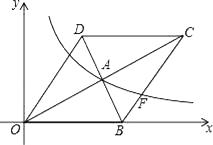
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个数用大括号围起来,中间用逗号断开,如:{1,2,﹣3}、{﹣2,7,![]() ,19},我们称之为集合,其中的每个数称为该集合的元素.如果一个所有元素均为有理数的集合满足:当有理数a是集合的元素时,2015﹣a也必是这个集合的元素,这样的集合我们称为好的集合.例如集合{2015,0}就是一个好的集合.
,19},我们称之为集合,其中的每个数称为该集合的元素.如果一个所有元素均为有理数的集合满足:当有理数a是集合的元素时,2015﹣a也必是这个集合的元素,这样的集合我们称为好的集合.例如集合{2015,0}就是一个好的集合.
(1)集合{2015}_____好的集合,集合{﹣1,2016}_____好的集合(两空均填“是”或“不是”);
(2)若一个好的集合中最大的一个元素为4011,则该集合是否存在最小的元素?如果存在,请直接写出答案,否则说明理由;
(3)若一个好的集合所有元素之和为整数M,且22161<M<22170,则该集合共有几个元素?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
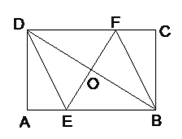
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括O、B),做MN⊥DM,垂足为M,交∠CBE的平分线于点N.
(1)求点C的坐标;
(2)求证:MD=MN;
(3)如图(2),连接DN交BC于F,连接FM,探究线段MF、CF、OM之间有什么数量关系?并证明你的结论.
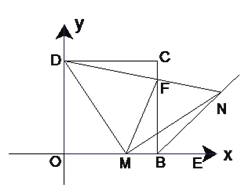
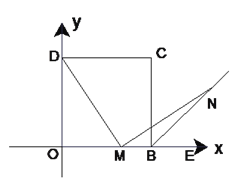
图(1) 图(2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别是BC、CD上的动点(不与点B,C,D重合),且∠EAF=45°,AE、AF与对角线BD分别相交于点G、H,连接EH、EF,则下列结论:① △ABH∽△GAH; ② △ABG∽△HEG; ③ AE= ![]() AH; ④ EH⊥AF; ⑤ EF=BE+DF
AH; ④ EH⊥AF; ⑤ EF=BE+DF
其中正确的有( )个。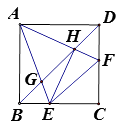
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=2,AC=![]() ,∠BAC=105°,△ABD,△ACE,△BCF都是等边三角形,则四边形AEFD的面积为__________.
,∠BAC=105°,△ABD,△ACE,△BCF都是等边三角形,则四边形AEFD的面积为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com