
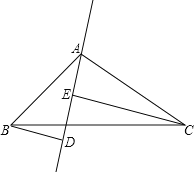
【题目】如图,正方形ABCD中,点E、F分别是BC、CD上的动点(不与点B,C,D重合),且∠EAF=45°,AE、AF与对角线BD分别相交于点G、H,连接EH、EF,则下列结论:① △ABH∽△GAH; ② △ABG∽△HEG; ③ AE= ![]() AH; ④ EH⊥AF; ⑤ EF=BE+DF
AH; ④ EH⊥AF; ⑤ EF=BE+DF
其中正确的有( )个。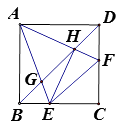
A.2
B.3
C.4
D.5
【答案】D
【解析】①BD是正方形ABCD的对角线,所以∠ABD=45°,
∵∠EAF=45°,∴∠ABD=∠EAF=45°.
∵∠AHB=∠AHG,∴ ![]() ABH∽
ABH∽ ![]() GAH,即①正确。
GAH,即①正确。
②四边形ABCD是正方形,BD为其对角线,所以∠DBC=45°.
∵∠EAF=45°,∴∠EAF=∠DBC.
∴ ![]() AGD∽
AGD∽ ![]() BGE,
BGE, ![]() ,即
,即 ![]()
∵∠AGB=∠HE,∴△ABG∽△HEG.
故②正确.
③由②知△ABG∽△HEG,则∠ABG=∠AEH.
易知∠ABG=45°,所以∠AEH=45°.
∵∠EAH=45°,∴ ![]() AEH是等腰直角三角形.
AEH是等腰直角三角形.
∴ ![]() =
= ![]() ,AE=
,AE= ![]() AH
AH
即③正确.
④由③知 ![]() AEH是等腰直角三角形,所以EH⊥AF,即④正确。
AEH是等腰直角三角形,所以EH⊥AF,即④正确。
⑤将△ADF绕点A顺时针旋转90°得到△ABM.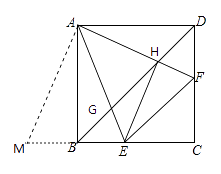
易知BM=DF,∠DAF=∠BAM,AF=AM
四边形ABCD为正方形,∠EAF=45°,则∠BAE+∠DAF=45°
即∠BAM+∠BAE=∠MAE=45°.
∵AE=AE
∴ ![]() AFE≌
AFE≌ ![]() AME,ME=EF.
AME,ME=EF.
∵ME=MB+BE=DF+BE
∴EF=BE+DF。
所以五个命题都是正确,答案为D.
根据相似三角形的判定,证明三角形相似。对于最后一问,注意问题的转化,通过作辅助线,证明ME=EF=EB+DF。


科目:初中数学 来源: 题型:
【题目】下列说法:(1)相反数是本身的数是正数;(2)两数相减,差小于被减数;(3)绝对值等于它相反数的数是负数;(4)倒数是它本身的数是1;(5)若![]() ,则a=b;(6)没有最大的正数,但有最大的负整数.其中正确的个数( )
,则a=b;(6)没有最大的正数,但有最大的负整数.其中正确的个数( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.例如正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.
(1)如果⊙P是以(3,4)为圆心,1为半径的圆,那么点O(0,0)到⊙P的距离为
(2)求点 ![]() 到直线
到直线 ![]() 的距离;
的距离;
(3)如果点 ![]() 到直线
到直线 ![]() 的距离为3,求a的值.
的距离为3,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2018次运动后,动点P的坐标是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在已知线段AB的同侧构造∠FAB=∠GBA,并且在射线AF,BG上分别取点D和E,在线段AB上取点C,连结DC和EC.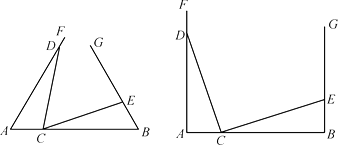
Ⅰ、如图,若AD=3,BE=1,△ADC≌△BCE.在∠FAB=∠GBA=60或∠FAB=∠GBA=90两种情况中任选一种,解决以下问题:
①线段AB的长度是否发生变化,直接写出长度或变化范围;
②∠DCE的度数是否发生变化,直接写出度数或变化范围.
Ⅱ、若AD=a,BE=b,∠FAB=∠GBA=α,且△ADC和△BCE这两个三角形全等,请求出:
①线段AB的长度或取值范围,并说明理由;
②∠DCE的度数或取值范围,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
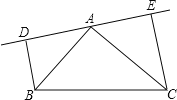
(2)若B、C在DE的两侧(如图所示),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运动品牌对第一季度A、B两款运动鞋的销售情况进行统计,两款运动鞋的销售量及总销售额如图10所示:
(1)一月份B款运动鞋的销售量是A款的![]() ,则一月份B款运动鞋销售了多少双?
,则一月份B款运动鞋销售了多少双?
(2)第一季度这两款运动鞋的销售单价保持不变,求三月份的总销售额(销售额=销售单价×销售量);
(3)结合第一季度的销售情况,请你对这两款运动鞋的进货、销售等方面提出一条建议。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为直角△ABC的斜边AB上一点,DE⊥AB交AC于E,如果△AED沿DE翻折,A恰好与B重合,联结CD交BE于F,如果AC═8,tanA═ ![]() ,那么CF:DF═
,那么CF:DF═ 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com