
【题目】如图,D为直角△ABC的斜边AB上一点,DE⊥AB交AC于E,如果△AED沿DE翻折,A恰好与B重合,联结CD交BE于F,如果AC═8,tanA═ ![]() ,那么CF:DF═
,那么CF:DF═ 
【答案】6:5
【解析】解:∵DE⊥AB,tanA═ ![]() , ∴DE=
, ∴DE= ![]() AD,
AD,
∵Rt△ABC中,AC═8,tanA═ ![]() ,
,
∴BC=4,AB= ![]() =4
=4 ![]() ,
,
又∵△AED沿DE翻折,A恰好与B重合,
∴AD=BD=2 ![]() ,DE=
,DE= ![]() ,
,
∴Rt△ADE中,AE= ![]() =5,
=5,
∴CE=8﹣5=3,
∴Rt△BCE中,BE= ![]() =5,
=5,
如图,过点C作CG⊥BE于G,作DH⊥BE于H,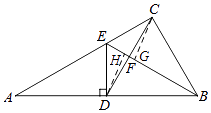
则Rt△BDE中,DH= ![]() =2,
=2,
Rt△BCE中,CG= ![]() =
= ![]() ,
,
∵CG∥DH,
∴△CFG∽△DFH,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() .
.
所以答案是:6:5.
【考点精析】根据题目的已知条件,利用翻折变换(折叠问题)和解直角三角形的相关知识可以得到问题的答案,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别是BC、CD上的动点(不与点B,C,D重合),且∠EAF=45°,AE、AF与对角线BD分别相交于点G、H,连接EH、EF,则下列结论:① △ABH∽△GAH; ② △ABG∽△HEG; ③ AE= ![]() AH; ④ EH⊥AF; ⑤ EF=BE+DF
AH; ④ EH⊥AF; ⑤ EF=BE+DF
其中正确的有( )个。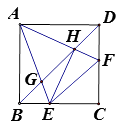
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=2,AC=![]() ,∠BAC=105°,△ABD,△ACE,△BCF都是等边三角形,则四边形AEFD的面积为__________.
,∠BAC=105°,△ABD,△ACE,△BCF都是等边三角形,则四边形AEFD的面积为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
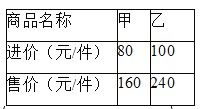
【题目】某商场同时购进甲、乙两种商品共![]() 件,其进价和售价如右表,设其中甲种商品购进
件,其进价和售价如右表,设其中甲种商品购进![]() 件.
件.
(1)直接写出购进乙种商品的件数;(用含![]() 的代数式表示)
的代数式表示)
(2)若设该商场售完这![]() 件商品的总利润为
件商品的总利润为![]() 元.
元.
①求![]() 与
与![]() 的函数关系式;
的函数关系式;
②该商品计划最多投入![]() 元用于购买这两种商品,则至少要购进多少件甲商品?若售完这些商品,则商场可获得的最大利润是多少元?
元用于购买这两种商品,则至少要购进多少件甲商品?若售完这些商品,则商场可获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节约意识,我市出台阶梯电价计算方案如下表:
价目表 | |
不超过 |
|
超过 |
|
超过 |
|
注:电费按月结算 | |
![]() 某户居民
某户居民![]() 月份应缴电费
月份应缴电费![]() 元,该户居民
元,该户居民![]() 月份用电多少度?
月份用电多少度?
![]() 某户居民
某户居民![]() 月份用电
月份用电![]() 度,应缴电费
度,应缴电费![]() 元,求
元,求![]() 的值;
的值;
![]() 用
用![]() (度)表示月用电量,请根据
(度)表示月用电量,请根据![]() 的不同取值范围用含
的不同取值范围用含![]() 的代数式表示该月应缴电费.
的代数式表示该月应缴电费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料
勾股定理神秘而美妙,它的证法多种多样,下面是教材中介绍的一种拼图证明勾股定理的方法.

先做四个全等的直角三角形,设它们的两条直角边分别为a,b,斜边为c,然后按图1的方法将它们摆成正方形.
由图1可以得到![]() ,
,
整理,得![]() .
.
所以![]() .
.
如果把图1中的四个全等的直角三角形摆成图2所示的正方形,
请你参照上述证明勾股定理的方法,完成下面的填空:
由图2可以得到 ,
整理,得 ,
所以 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出如下结论:①单项式﹣![]() 的系数为﹣
的系数为﹣![]() ,次数为2;②当x=5,y=4时,代数式x2﹣y2的值为1;③化简(x+
,次数为2;②当x=5,y=4时,代数式x2﹣y2的值为1;③化简(x+![]() )﹣2(x﹣
)﹣2(x﹣![]() )的结果是﹣x+
)的结果是﹣x+![]() ;④若单项式
;④若单项式![]() ax2yn+1与﹣
ax2yn+1与﹣![]() axmy4的和仍是单项式,则m+n=5.其中正确的结论是_____(填序号)
axmy4的和仍是单项式,则m+n=5.其中正确的结论是_____(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m﹣1)x+m2=0有两个实数根x1和x2 .
(1)求实数m的取值范围;
(2)当x12﹣x22=0时,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com